Lab 10: Heaps and priority queues

The goal of this lab is to learn the specification, an implementation, and the uses of the priority queue abstract data type.

1. Introduction

Refer to the prelab reading to review introductory information about priority queues and heaps.

2. Setup

I am providing a bunch of code for you. Clone the lab10 repository from the class directory:

hg clone /cslab/class/csci245/lab10

That will give you a lab10 directory, with the source files in package (subdirectory) heap.

3. The Heap class

The abstract class Heap contains the basic functionality for a heap that you will extend to make a priority queue. It already has an internal array as an instance variable (plus a heapSize variable that tells how much of the array is in use) and helper methods to calculate the children and parent from a given index. (The math for calculating children and parents is a little different to make up for the fact that we do not have an unused position at 0.)

What you need to provide for the heap is the implementation for a helper method heapify(), which we call on a heap given a node identified by its index. heapify() enforces the heap property on the tree rooted at the given index—under certain assumptions. This method can be used to set up the array so that it satisfies the heap property, or it can be used to fix up the heap if some other operations result in a violation of the heap property.

This method assumes that both subtrees of the given node satisfy the heap property (they are greater than their children, etc), but the given node might violate it; it might be smaller than one or both of its children. heapify() fixes up the subtree rooted at the given node by pushing it down until there no longer is a violation.

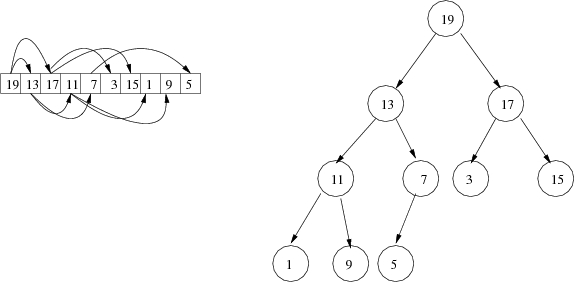
Consider again the example heap from the pre-lab reading:

Now consider what happens if you replace the 19 at the root with the value 10, giving the leftmost tree below. If you look at the two subtrees below the root (element index 1, value 13, and element index 2, value 17), you can see that each of those subtrees still satisfies the heap property. The only violation is at the root (index 0, value 10), which is smaller than both of its children.

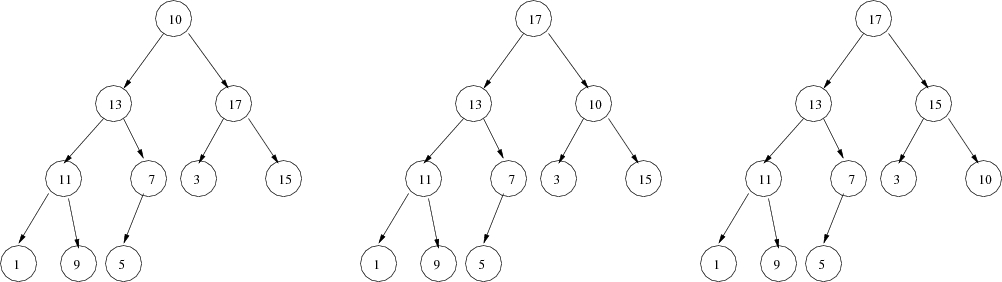
This is exactly the condition that heapify(0) is supposed to fix. It does it by swapping the out-of-place element with one of its children (which one?) so that the correct relationship between parent and immediate children is established, producing the center picture above. The heap property still holds in the subtree that was not changed (under 13), but the swap may have created a new violation at the root of the subtree where the new value was moved (value 10, index 2, the right subtree). So now that subtree needs to be fixed up with a call to heapify(2). That does another swap, producing the right-hand picture. If we check where the value 10 has now landed, we find that it does not have any children that are larger; so now we know that the heap property applies everywhere.

Write this method and compile. The file Test.java contains a program to test your work as you go along, but it does not contain anything to test heapify() by itself; you will test it along with the next section.

I have provided two extra methods in Heap, however, that you may find helpful as you do your testing. The method checkHeap() can be used to check whether a subtree satisfies the heap property. If you pass it true for its verbose parameter, it will also print out where in the heap it detects a violation. The method toString() provides a convenient way to turn a heap into something that can be printed.

Methods like these are often called scaffolding. They won't be called anywhere when you've completed the lab, but they provide ways to display state and to check properties. Even though it means writing more code, providing scaffolding often gets you a working program faster than if you try to work without it.

4. Excursus: Heapsort

Before we implement priority queues, we'll explore a bonus application of heaps: A nifty and very efficient sorting algorithm, called heapsort.

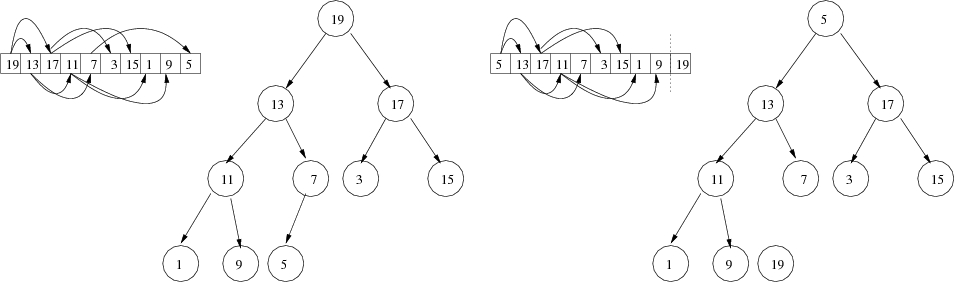
Now 19 is correctly placed in the array, but we no longer have a heap because 5 is in violation. So we call heapify() with the root to fix up the violation incurred. We repeat this whole process (swapping the root with the last leaf, then heapifying) until the heap is "empty"—although the array is still full, it's just that none of it is counted as part of the heap.

The method sort() in class HeapSorter is static, but it instantiates subclass HeapSorter of Heap to store its data. Complete the constructor of this class so that it initially converts an array into a heap (using repeated and strategic calls to heapify()— think about this carefully) and write the code for the sort() method, using the strategy described above.

Hint: heapify() requires a node for which the subtrees already satisfy the heap property. If you fill the array for a heap with random values, are there any subtrees that automatically (not merely accidentally) satisfy the heap property? How can you use that observation to apply heapify()? It may help to draw pictures of some trees.

Then test your work using the Test program. Open it to see how it works. By running

java heap/Test heapsort

it will sort an array and print out the sorted version. The correct result is

11 22 33 44 55 66 77 88 99 

Use the scaffolding as needed to check your assumptions and to see what is going on.

5. Class PriorityQueue

Now we will implement the priority queue class. This also is an extension of the Heap class. The isEmpty(), isFull(), and max() methods are easy and already completed for you. What remains is code for adding and removing elements.

First, adding an element. Our strategy is simply to place it in the next available position in the array and increment the size of the heap. This may result in a violation of the heap property—the new element may be larger than its parent. If that happens, then we move the new element up the tree until it is in an appropriate place. Consider the following illustration of adding the element 16:

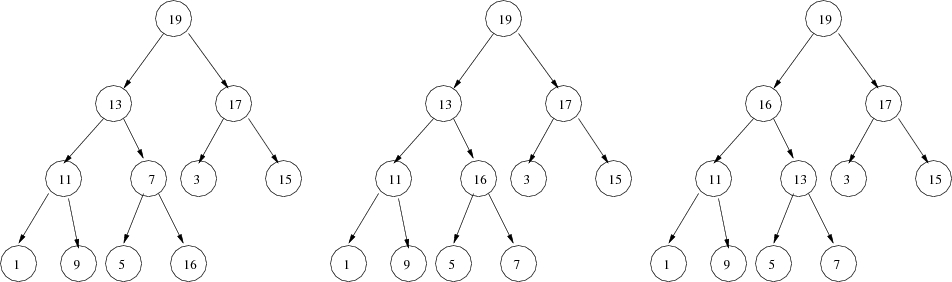
Next, removing the maximum element. Our strategy is to copy the last element in the heap to the first position in the array and then decrease the size of the heap, as illustrated here.

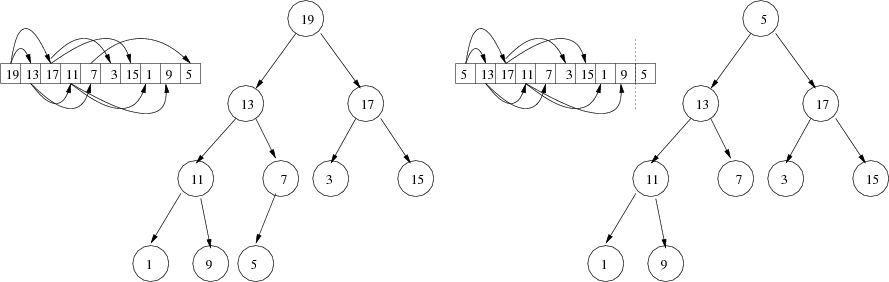
Then use heapify() to correct the violation incurred.

Implement these two methods, then test it using java heap/Test pq. The correct result is

33 99 88 77 66 55 44 22 11

6. Using a priority queue to implement a queue

To take us back around to stacks and queues, consider how a priority queue can be used to implement a queue: As each element is entered into the priority queue, it is assigned a priority based on its time of arrival. This implies that the element is distinct from its priority—different from the examples we've seen so far where the element is an integer which is used as its priority.

To get around this, the class Queue has two instance variables—a PriorityQueue and a HashMap. The HashMap associates priorities with elements, and the PriorityQueue stores priorities.

Consider this scenario. An element, say 3, is entered into the queue. It is assigned a priority 15. Thus we insert 15 into the PriorityQueue and associate 15 with 3 in the HashMap. Sometime later, removeFront() is called on the Queue, which in turn calls extractMax() on the PriorityQueue, which returns 15. We then lookup 15 in the HashMap and find 3; 3 then is the value returned from removeFront().

The real trick to all this is determining how to assign priorities.

Implement what's left in the Queue class, and test it using java heap/Test queue. The correct result is

33 22 66 99 11 88 55 77 44

7. Using a priority queue to implement a stack

Finally, do the same thing as in the previous section, but implement a stack. The only real difference is how you assign priorities. Test using java heap/Test stack. The correct result is

22 11 77 44 55 88 99 66 33

8. Handing in

Be sure that you have everything committed to your Mercurial repository. Then, from your lab10 directory, turn it in with

/cslab/class/csci245/bin/handin lab10 .hg heap/*.java

Be sure that both partners have a copy of the code before you leave.