The goal of this project is reinforce the work on sorting arrays by implementing the mergesort and quicksort algorithms and to conduct a careful empirical study of the relative performace of sorting algorithms.
Your work will be threefold:
Recall the difference between insertion and selection sorts. Although they share the same basic pattern (repeatedly move an element from the unsorted section to the sorted section), we have
Insertion
Selection
Now, consider the basic pattern of merge sort:
More specifically, merge sort splits the array simplistically (it's the "easy" part). The reuniting is complicated. What if there were a sorting algorithm that had the same basic pattern as merge sort, but stood in analogy to merge sort as selection stands towards insertion? In other words, could there be a recursive, divide-and-conquer, sorting algorithm for which the splitting is the hard part, but leaves an easy or trivial reuniting at the end?
To design such an algorithm, let's take another look at what merge sort does. Since the splitting is trivial, the interesting parts are the recursive sorting and the reuniting. The recursive call sorts the subarrays internally, that is, each subarray is turned into a sorted subarray. The reuniting sorts the subarrays with respect to each other, that is, it moves elements between subarrays, so the entire range is sorted.
To rephrase our earlier question, the analogue to mergesort would be an algorithm that sorts the subarrays with respect to each other before sorting each subarray. Then reuniting them is trivial. The algorithm is called "quicksort," and as its name suggests, it is a very good sorting algorithm.
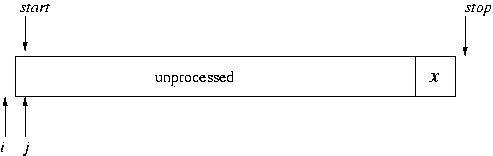
Here's a big picture view of it. Suppose we have an array, as pictured below. We pick one element, x, and delegate it as the "pivot." In many formulations of array-based quicksort, the last element is used as the pivot (though it doesn't need to be the last).

Then we separate the other elements based on whether they are greater than or less than the pivot, placing the pivot in the middle.

In a closer look, while we do this partitioning of the array, we maintain three portions of the array: the (processed) elements that are less than the pivot, the (processed) elements that are greater than the pivot, and the unprocessed elements. (In a way, the pivot itself constitutes a fourth portion.) The indices i and j mark the boundaries between portions: i is the last position of the portion less than the pivot and j is the first position in the unprocessed portion. Initially, the "less than" and "greater than" portions are empty.
During each step in the partitioning, the element at position j is examined. It is either brought into the "greater than" portion (simply by incrementing j) or brought into the "less than" portion (by doing a swap and incrementing both i and j).
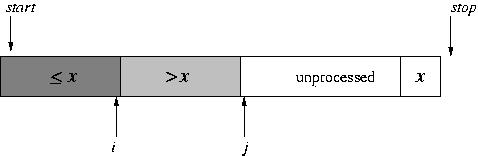
(Think about that very carefully; it's the core and most difficult part of this project.)
At the end, the unprocessed portion is empty.

All that's left is to move the pivot in between the two portions, using a swap. We're then set to do the recursive calls on each portion.
Make a directory for this course (if you haven't already). Make a new directory for this project. Then copy into it some starter code, which will be similar to the code you started with in lab.
cd 245 mkdir project1 cd project1 cp /cslab/class/csci245/project1/* .
You will also need to write a makefile.
This is not only for your convenience; it also will be part of what you're
graded on.
You might still need to take the time to reason through how a makefile works
(and how compiling and linking in C work).
I recommend that you write your makefile from scratch as a learning
exercise, but you can also look at the makefile from lab 2 if you are stuck
(or compare yours with that one to make sure you're on the right track).
The one from lab 2 will be pretty similar to the one you write for this
project.
It can be found at /cslab/class/csci245/lab2/makefile.
Notice that I have given you arrayUtil.c this time; so
you will need to include a rule to compile it into an object file.
We talked about mergesort in class, and in sorts.c
you will find (unfinished) code for mergesort.
In fact, there are two functions with mergeSort
in the name.
The function mergeSort() corresponds to the
prototype for mergesort found in sorts.h
and used in the driver sDriver.c
It is finished.
It starts the recursive process by calling
mergeSortR(), which is the one you need to finish.
Notice that mergeSortR() takes not only an array
but also a starting point and an stopping point.
This is the range in the array that this call to mergeSortR()
needs to sort.
start is inclusive, stop is exclusive.
Specifically, you need to write the part the does the merging.
You will need to make use of a helper array, which you can allocate
using blankArray() from the arrayUtil
library.
You will also need to write merge sort in such a way that
you tally the number of comparisons and so that mergeSort()
returns the number of comparisons.
Use sDriver to confirm that your algorithm
sorts correctly.
As with mergesort, there are two functions with quickSort
in their name.
The second function corresponds to the
prototype for quick sort found in sorts.h
and used in the driver sDriver.c
It is finished.
It starts the recursive process by calling
quickSortR(), which is the one you need to finish.
As with mergesort, quickSortR() takes not only
an array but also a starting point and a stopping
point in the array.
As with the other sorts, tally the number of comparisons.
Use sDriver to confirm that your algorithm
sorts correctly.
As we have been talking about in class, merge sort and quick sort are in different "complexity classes" in terms of the their worst case performance. Merge sort is O(n lg n), whereas quicksort is O(n^2). (O(n lg n) is faster). However, these are worst cases; we might find that experimentally one of the algorithms may behave better on average.
Write a program or programs to automate experiments to compare both the running time and number of comparisons for quicksort, mergesort, shell sort, selection sort, insertion sort, and bubble sort.
This time, in addition to counting comparisons,
we'll take actual time measurements.
arrayUtil has a function getTimeMillis().
It returns the number of milliseconds that have elapsed since
midnight, Jan 1, 1970---the standard way to do time keeping on
many computer platforms.
By calling this function before and after sorting and taking the
difference, we can compute how long it takes to do the sort.
Use several different arrays of several sizes, and compare the results for the different algorithms.
Write a few paragraphs explaining how you did your experiment and what your findings are. Present your data using a table and one or more graphs.
Turn in your code (including the makefile), results, and write-up by
copying them all to a new directory; cd into that
directory, and then do
/cslab/class/csci245/bin/handin project1 .Notice the 'dot' at the end of the command; that tells it to hand in the entire directory.
DUE: Tuesday, Feb 5, 5:00 pm.