CSCI 235 Lab 6: Introducing recursion

You will be working with your partner on one of your accounts.

This lab introduces the idea of writing recursive methods.

1. Setup

Move to your directory for this class. Clone the provided repository to get the starting point for this lab.

That makes a new directory lab6, where you will be working today.

2. Initial examples

Open the file Examples.java in Emacs.

2.1 probA() and countDown()

Compile and run Examples.java. It includes the method probA() from your assignment

In its initial form, the program calls this method with the arguments 0, 3, and 4.

Now look at the method countDown(), which is almost the same. The key differences are that this method prints something at the beginning and end of every call, and the additional parameter indent is used to help you see the way that the lines printed are related. Go to main() and comment out the call to showProbA() and uncomment showCountDown(). When you (compile and) run it now, what you’ll see for the call with 3 looks like this:

This shows how the activation of countDown() for 3 calls the one for 2, and so on until the call for 0. We often describe uutput that shows the intermediate steps in a computation as tracing the execution.

2.2 probC()

A recursive method can have more than one base case, as shown in probC(). You can uncomment the call to showProbC() to see what it prints.

The method probCx() does the same thing, but prints at the beginning and end of each call (using an extra parameter to indent nicely). Uncomment the call to showProbCx() to see the steps along the way.

2.3 probCy()

This is a slight rewrite of the previous method so that the tracing can turned on or off by providing the indentBy parameter. You can see how this works by selectively uncommenting the calls to showProbCy() in main().

Make sure that you understand how this works, because it is part of the framework you will use in the next section.

3. Writing your own

Now it is your turn. Open the file Euclid.java. Your job will be to write a method that recursively computes the greatest common divisor of two positive integers. Do this without looking at the code from class.

Before you work on that, notice that I have set up the main method so that you can run the program with two or three arguments. The first argument turns into the parameter m, and the second becomes n. The third parameter—if you supply one—should be yes or no, to indicated whether you want tracing output. If you include yes, you should see tracing output; if no you should not.

So you should (eventually) be able to run your program with

to see just the result, or with

to see it with a trace of calls.

I have also provided you with a a file Euclid2.class to help you check your answers. Your program should produce the same output as that program.

3.1 A tracing version

It is easier to work on something when you can see how it works. You have been provided with a start on method named traceGcd(); it already has the printing and indenting framework that you saw in the last example method. What you need to do is fill in the middle of this method so that it sets result to the value that should be returned.

Note: you should not use any loop, nor should you write a return statement.

Expressed recursively, Euclid’s algorithm for computing the greatest common divisor of m and n is based on the following observations:

• If m and n are the same, either of them is clearly their gcd.
• If they are not equal, their gcd is the same as the gcd of the smaller of the two and their difference (larger minus smaller).

Complete traceGcd() and verify that it works correctly (both tracing and not tracing). Pay attention to the comments in traceGcd().

3.2 Cleaning it up

After you have that working, copy the code into the non-tracing version gcd(), getting rid of the extra stuff. Don’t forget to change any recursive calls.

If its third command-line argument is x, the program Euclid will call the non-tracing version. Make sure that it works.

4. Bonus challenge

The Fibonacci sequence is defined by

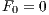
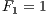
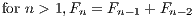
The file Fib.java provides a framework similar to that in Euclid.java; it should recursively compute the nth Fibonacci number if run with So you should (eventually) be able to run your program with, for example,

where the numeric parameter is the value for n and the last parameter controls tracing, as for the previous program.

So write the tracing method traceFib() and, time permitting, the non-tracing version fib(). I’ve provided you with Fib2.class so that you can see the correct results.

5. Turn in

Commit your changes to Mercurial.

Create a script file to show your program compiling and running. Run Euclid so that it calls the tracing version of your method for several different values of m and n, with and without tracing. Then run Euclid again for the same set of values, but with a third argument of x so that it calls the non-tracing version of your method.

If you had time to work on Fib, include compiling and running it in your trace, too.

Turn in Euclid.java (and Fib.java if you worked on it) and your script putput as lab6. Do not turn in a printed copy.

Copy the repository to the other partner’s account.