Sorting arrays

1. Introduction

In computing, sorting means the process of putting a collection of things into order.¹ Sorting is a fundamental problem in computer science. Not only do many applications require putting data in order, but also sorting is a good case study for problems and algorithms. There are many ways to sort a set of data—some ways are more intuitive (that is, easier for a human to understand) than others, some are faster than others, and some require more computer memory than others. This handout describes three algorithms for sorting arrays of integers. We’ll write code for the first one in class; you’ll be writing the other two as part of a project.

To get used to the idea, you may find it helpful to try sorting numbers by hand. For example, take a pile of index cards and write a number on each of them. Lay them out in a row on a table, and then start rearranging them to put them in order. Pay careful attention to the steps you take, including which positions you need to keep track of. How would you instruct another person to sort a row of cards using the same process that you used? We are going to be thinking here about how a computer should sort an array of numbers.

2. Bubble sort

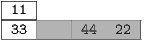
The algorithm called bubble sort is not a particularly efficient algorithm (in fact, it’s one of the worst), but it is very easy to understand and to program, so we will start with it. The idea is to iterate through the array and to compare adjacent elements, swapping them if they are out of order. Consider this example on an array containing the values 33, 11, 44, 22. When we start, we don’t know anything about how they are ordered, which we’ll indicate by coloring them gray.

We’ll begin at the left end, comparing the first two elements. In this case, they are out of order; so we swap them.

We move one place to the right, and see that we do not need to swap 33 and 44:

Moving right again, we see that we need to swap the last two elements:

After that, we know that the biggest element has reached the right end, where it belongs. So we will color it white.

Notice that one pass through the array is not enough. In fact, we’ve placed only a single element in the right place.

We start again at the left end, comparing and swapping our way through the three elements that are not known to be sorted.

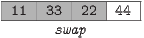
We need to start at the left one more time to see whether the first two elements are in the right order:

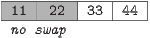
Each pass gets another element into the correct place; so now the three biggest are where they belong.

If all but one element are in their correct places, then that last element has nowhere to be but where it belongs. So we are done:

Notice how the process makes a pass through the array once for each position in the array—we end up with a loop within a loop.

3. Selection Sort

If you start with the unsorted collection of cards in your hand, you could look through it to find the smallest number. When you find the smallest, you take it our of your hand and put it into an ordered group on the table. Then you find the smallest number still in your hand and place it after the card on the table. Repeat as long as you have cards in your hand; when you finish, you will have moved the cards from an unsorted group (your hand) to the ordered group on the table. This is called selection sort because each time you

Think about how to do this on the computer using arrays. You might think about using two arrays, one for sorted and one for unsorted. But because the total number of numbers stays the same, we can treat it as having a “sorted” section at the left and an “unsorted” section at the right. We start off with no elements in the sorted section; on each pass through the array, we will make the sorted section one larger.

We search the the unsorted section (the entire array) for the smallest value. When we find the smallest, we swap that value with the one in the first position of the unsorted section. Because that is the smallest, it is now in the correct place; so the sorted section grows by one, and the unsorted section shrinks by one element. As before, we will color the unsorted section gray.

We note that the smallest unsorted element is 11:

We swap it into the first place, giving us

Find the smallest gray value:

and swap again.

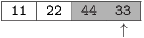
Find the smallest and swap

We are down to one element, which has to be in the right place; so we are done.

4. Insertion sort

Insertion sort works this way: you take cards one at a time from an unsorted sequence and place each into the correct place in an already sorted sequence. For example, here we have an initially empty sorted group on the left and the cards 33, 11, 44, 22 in the unsorted group on the right:

You pick up the first card from the unsorted group, 33, and place it in the sorted group. Since 33 is all by itself, it is “sorted.”

Next you pick the next unsorted card, 11.

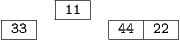
You put 11 into the correct position in the sorted group by putting it in front of the 33.

Next, pick up 44. Since it is larger than 11 and 33, you put it after the 33.

Finally, you pick up 22:

You insert it between 11 and 33.

In the end, the unsorted group is empty, and the sorted group contains 11, 22, 33, 44.

For efficiency we use a single array instead of having two separate groups. We treat the left end of that array as the sorted part, and the right end as the unsorted part (in gray). Initially, the sorted part is empty and the unsorted part is the entire array.

But as we noted above, you can declare the first element to be sorted.

Now we take the first element from the unsorted section.

We compare it with each already-sorted element, starting at the right end. If it is smaller, we scoot that element up and move to the next place.

When we find a smaller value—or run out of places—we put the element we are holding into the “vacant” spot.

Moving up one place:

We compare and do not scoot; so we end up putting 44 back where it was:

And, finally, we take the last value, 22, and insert it properly: