The goal of this project is reinforce the work on sorting arrays and lists by implementing the quicksort algorithm.
Recall the difference between insertion and selection sorts. Although they share the same basic pattern (repeatedly move an element from the unsorted section to the sorted section), we have
| Insertion | Take the next unsorted item (easy) | put it in the right place (hard) |
| Selection | Take the smallest unsorted item (hard) | put it in the next place(easy) |
Now, consider the basic pattern of merge sort:
| split | sort the pieces recursively | reunite |
More specifically, merge sort splits the array simplistically (it's the "easy" part). The reuniting is complicated. What if there were a sorting algorithm that had the same basic pattern as merge sort, but stood in analogy to merge sort as selection stands towards insertion? In other words, could there be a recursive, divide-and-conquer, sorting algorithm for which the splitting is the hard part, but leaves an easy or trivial reuniting at the end?
To design such an algorithm, let's take another look at what merge sort does. Since the splitting is trivial, the interesting parts are the recursive sorting and the reuniting. The recursive call sorts the subarrays internally, that is, each subarray is turned into a sorted subarray. The reuniting sorts the subarrays with respect to each other, that is, it moves elements between subarrays, so the entire range is sorted.
To rephrase our earlier question, the analogue to mergesort would be an algorithm that sorts the subarrays with respect to each other before sorting each subarray. Then reuniting them is trivial. The algorithm is called "quicksort," and as its name suggests, it is a very good sorting algorithm.
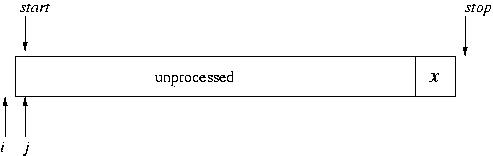
Here's a big picture view of it. Suppose we have an array, as pictured below. We pick one element, x, and delegate it as the "pivot." In many formulations of array-based quicksort, the last element is used as the pivot (though it doesn't need to be that way).

Then we separate the other elements based on whether they are greater than or less than the pivot, placing the pivot in the middle.

In a closer look, while we do this partitioning of the array, we maintain three portions of the array: the (processed) elements that are less than the pivot, the (processed) elements that are greater than the pivot, and the unprocessed elements. (In a way, the pivot itself constitutes a fourth portion.) The indices i and j mark the boundaries between portions: i is the last position of the portion less than the pivot and j is the first position in the unprocessed portion. Initially, the "less than" and "greater than" portions are empty.
During each step in the partitioning, the element at position j is examined. It is either brought into the "greater than" portion (simply by incrementing j) or brought into the "less than" portion (by doing a swap and incrementing both i and j).
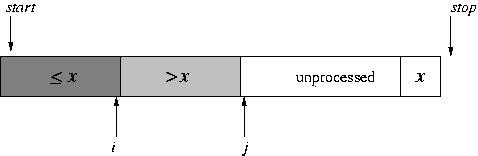
(Think about that very carefully; it's the core and most difficult part of this project, at least for the array version.)
At the end, the unprocessed portion is empty.
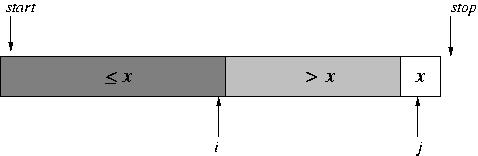
All that's left is to move the pivot in between the two portions, using a swap. We're then set to do the recursive calls on each portion.
Make a new directory for this project.
Then copy into it SortUtil.java and Node.java
from lab 2.
cd 245 mkdir proj1 cd proj1 cp /cslab/class/cs245/lab2/SortUtil.java . cp /cslab/class/cs245/lab2/Node.java . cp /cslab/class/cs245/lab2/IntListPair.java .
Write a class with a sort() method that
uses the quicksort algorithm to sort arrays (and counts comparisons).
Use the description of the algorithm above as a guide.
Test your method to make sure it works--- either
write a simple driver yourself (which you do not need to turn in)
or use the SortArray class from the labs.
Now write another class, this time with a list version
of quick sort.
You may want to use the first element as a pivot this time.
Again, test your method with your own driver or
SortList.
As we will be talking about in class while you work on this project, merge sort and quick sort are in different "complexity classes" in terms of the their worst case performance. Merge sort is O(n lg n), whereas quicksort is O(n^2). (O(n lg n) is faster).
Write a program or programs to automate experiments to compare the running time and number of comparisons for quicksort and mergesort, both for arrays and lists. Use System.currentTimeMillis(). Compare their performance on the same array or list, that is, generate a random array, make a copy of it, and then both quicksort and mergesort it.
To reduce noise, make sure you are the only person using your workstation, and close all other programs.
Print out the files you wrote.
The command to print files neatly, two to a page, is a2ps.
Give this command the name of a printer using the -P
flag (the printer in the computer science lab is called sj),
and list all the files you want printed.
The flag --file-align=fill tells it not to start each file on
a new page, so less paper is wasted.
Furthermore, write a couple of paragraphs explaining how you did your experiment and what your findings are. You may want to include a table or graph.
DUE: Wednesday, Sep 12, 5:00 pm.