Project 3: Sorting arrays

The goal of this lab is to implement basic sorting algorithms. This will review and reinforce your understanding of how to manipulate arrays as well as give you practice in the basic syntax of writing methods.

SPECIAL NOTE

Beginning with this project, documentation and style will be assessed as part of your grade. Make sure you conform to conventions for identifiers and properly document all parts of your program.

1. Introduction

Sorting is a fundamental problem in computer science. Not only do many applications require putting data in order, but also sorting is a good case study for problems and algorithms. There are many ways to sort a set of data--- some ways are more intuitive (that is, easier for a human to understand) than others, some are faster than others, and some require more computer memory than others. This project description will describe three algorithms for sorting arrays of integers. The first of these three we will implement during class on Wednesday. The other two are yours to implement.

To get used to the project, you may find it helpful to try sorting numbers by hand. For example, take a pile of index cards and write a number on each of them. Then sort the pile. Pay careful attention to the steps you take. How would you instruct another person to sort a pile of cards using the same process that you used? In this lab you will think about how a computer should sort and array of numbers.

2. Setup

As, usual, move into your cs235 directory, make a directory for this assignment, and change into it.

cd cs235
mkdir proj3
cd proj3

I'm giving you code to start with. Copy those files from the course directory.

cp /homes/tvandrun/Public/cs235/proj3/* .

The file Sort.java is a "driver" program-- it's used to test out the things you will be writing. You will not need to modify this file at all; in fact, very little of it will you be able to understand (but just for the fun of it, open it in xemacs and look it over; marvel at all the code you will be able to understand--- and write yourself--- some day if you stick with it). What it does is test drive a sort algorithm by creating an array of size 10 randomly filled with integers from 0 to 99. Compile it, but don't bother running it yet.

You will write the implementation of sorting algorithms each in its own file.

3. Bubble sort

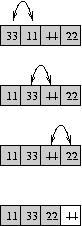
The algorithm called Bubble sort is not a particularly efficient algorithm (in fact, it's one of the worst), but it is very easy to understand and to program, so we will start with it. The idea is to iterate through the array and to compare adjacent elements, swapping them if they are out of order. Consider this example on an array containing the values 33, 11, 44, 22.

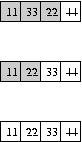
In the left column, we see what happens during one pass through the array. 33 is compared with 11; since they are out of order, they are swapped. Next, 33 is compared with 44; since they are in order, they are not swapped. Finally, 44 is compared with 22; since they are out of order, they are swapped. 44, the largest number, has made it all the way to the end of the array, so it is in the right place. The shaded are of the array is still unsorted, but the white area is sorted.

Notice that one pass through the array is not enough. In fact, we've placed only a single element in the right place. The right column shows the state of the array after successive rounds of the process we just described. If we pass through the entire array, we will place 33 in the second-to-last position. If we pass through again, we will place 22 in the third-to-last position.

Notice that this requires a loop within a loop--- an inner loop which conducts the pass over the array and an outer loop which repeats those passes.

The file Bubble.java contains a method sort() which takes an array and rearranges it so that it is sorted. We will look at this method in class on Wednesday. It does not contain a main() method because we will not run it as a stand-alone program. Instead, the main() method in Sort will invoke this method.

To try it out, compile the file as usual. To run it, do

java Sort Bubble

This will print the array before and after this sort() method runs.

4. Selection Sort

Our second alorithm, Selection sort works this way. Suppose again than you have a pile of cards in your hand, each with a number on it, which you would like to set in order. You might try flipping through the pile searching for the smallest. Once you find the smallest number, you could remove its card and set it in a new pile by itself--the new, sorted pile. Then you would flip through the original pile to find the next smallest number, and put its card next on the pile. By continuing this process, eventually you will transfer all the cards from the old, unsorted pile to the new, sorted pile.

Now think about how to do that in a computer program on arrays. The array is like a pile. The obvious, analogical way to do selection sort would be to create a second array (standing for the new pile) and repeatedly copy values from the old array to the new array, starting from smallest and continuing to the largest. However, to be efficient, we want to avoid making that extra array. Here's how:

We will consider the array at all times to have a "sorted" section and an "unsorted" section, just like we saw how Bubble sort worked. Before we begin, the sorted part will be empty, and the whole array will be the unsorted section. While the sorting happens, the sorted section will "grow", that is, it will comprise a larger and larger portion of the array; the unsorted section likewise will shrink. When we finish, the sorted section will take up the entire array and the unsorted section will be empty.

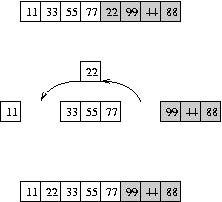
Assume that the sorted part comes first and the unsorted part is the rest. Then we search the array looking for the smallest number. When we find it, we swap that value with the value in the first position in the unsorted part. That way the sorted part of the array grows by one element and the unsorted shrinks by one element. Follow how it works in this illustration; the unsorted portion of the array is in gray.

Initially everything is unsorted. We identify 11 as the smallest and swap it with the first unsorted value, 33. Now 11 is in the correct position, so the sorted portion of the array is the first position. Next we find 22 as the smallest element in the unsorted part. We swap it with the first unsorted position, and so the sorted portion grows by one. Eventually, all elements are sorted.

Open the file Selection.java in Xemacs. You'll see that it contains an empty method sort(). You will need to fill in the method. You can compile and run the program now.

javac Selection.java
java Sort Selection

The program won't crash, but it won't sort the array either. Remember that anytime you make a change to Selection.java, that's the file you need to recompile, but you do not need to recompile Sort.java (because you're not going to make any changes to it).

Follow these steps to write a selection sort program:

1. Write a loop that simply finds the smallest value and prints it out. Since finding a smallest value is part of selection sort, this is a way to break down the problem--- plus it's review. If you compile an run at this point, you'll see that the array doesn't change before or after your method runs, but the smallest value of the array is printed out.
2. Next change what you've done so that your program does not ever record the smallest value, but instead records (and prints) the position (ie, index) of the smallest value.
3. Finally, the loop you have written so far must become the inner loop of the larger algorithm. Write the outer loop, which iterates over the array and, at each iteration, finds the position of the smallest unsorted value and swaps it with the value at the current position (notice that for each iteration of the outer loop, the current position is the first position in the unsorted section). Hint: you will have to change the starting index of the inner loop for this to work.

Compile, test, run, and when you're confident it's working right, move on.

5. Insertion sort

To set up this part, open the file Insertion.java.

Insertion sort works this way: If you were using insertion sort over a pile of cards, you would place cards in a new, sorted pile. You would take the next card on the unsorted pile and seach for the correct position in the sorted pile. For example, if you had cards with numbers 33, 11, 44, 22, initially they would all be in the unsorted pile. First, you pick up the card on top of that pile, 33, and place it in a new, sorted pile. Since 33 is all by itself, it is "sorted." Next you pick the next card in the pile, 11. You put 11 into the correct position in the sorted pile by putting it on top of the 33. Next, pick up 44. Since it is larger than 11 and 33, you put it under the 33. Finally, you pick up 22, and since it is between 11 and 33, you insert it between those cards in the pile. In the end, the unsorted pile is empty, and the sorted pile contains 11, 22, 33, 44.

For efficiency, we do not use two arrays, as you would use two piles. Instead, again consider the array to have two parts at any moment in the computation, a sorted part and an unsorted part. Initially, the sorted part is empty and the unsorted part is the entire array.

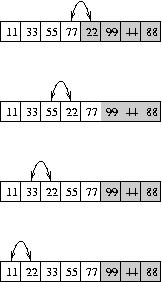
So, insertion sort maintains sorted and unsorted sections of the same array, and the sorted section grows at each step and eventually the whole array is sorted. It takes the first element in the unsorted section, and then shifts over part of the sorted section to make room for it. Consider this illustration. The left side shows a "big-step" view; the right side shows the same process in slow-motion.

Notice that in the "slow motion" version of the illustration, the way we move numbers over to make room is that we actually shift the new number over one space at a time (by swapping, like we did for Bubble sort) until it is in the right position.

Code insertion sort in your file and test it.

6. Turn in

Create the script file as before (cat, compile, and run). Run each sort a couple of times.

 a2ps (the name of the script file)

DUE: Wednesday, Sept 30, at 5:00 PM.