The goal of this lab is to practice implementing a hash table (or hash map), a final topic in the theme of abstract data types and their implementations.
This lab has some similarities to Project 3 (linked list implementation of a map in Java) and Lab 8 (sorted list map with generics, also in Java). The difference is that it will be in C and, generally, a little harder.
This pre-lab reading reviews many things from class on Friday, but since this is a difficult topic, it's important to read it thoroughly. If you read better on paper than on a screen (most people do), don't be shy about printing this out and reading it all first. Paper is a sustainable, renewable, recyclable, and compostable resource. It's okay to use it. You are also strongly encouraged to review your code for Project 3.
We have seen five abstract data types (ADTs): lists, maps, sets, stacks, and queues. We have also seen that each of these can be implemented using either a linked list or an array. In Project 3, you implemented a map using a linked list. The figure below shows on the left a map visualized abstractly as a table; on the right, a diagram illustrates how a linked list implementing this table might be arranged.

Remember the advantages and disadvantages of arrays vs linked lists. Jumping to a position in an array is fast, O(1), because of random access, but inserting or removing things in an array is slow, O(n). Inserting or removing things in a linked list is fast, O(1) if you have already found the place to insert or remove, but finding something in a linked list is slow, O(n), because of sequential access.
Think about the operation of looking up a value for a key in a list using a linked list like what you did in Project 3, where the nodes each contain a key and a value. One would need to step through the nodes in the linked list, checking each key until the right one is found. That's O(n).
O(n) might not seem so slow at first glace---after all, merge sort is O(n lg n) and selection sort and insertion sort are O(n^2). But keep in mind that map operations are not stand-alone algorithms but are operations that would be used in an algorithm. Thus if an O(n) operation happens inside a loop with O(n) iterations, the running time of the loop becomes O(n^2). For many purposes, that's just too slow.
What we want is an implementation of a map whose operations are constant time, O(1). To do this, we'll need to use an array so we can use random access. When we look up a value for a key, we want to be able to jump right to a position in the array.
But how can that be done?
If we kept all the keys in an array, we would still need to
search that array for the right key, and that would still be
O(n).
The trick is that since all information stored on a computer
can be broken down into numbers, and so we can
use the key to compute a number which we'll use as an
array index.
For example, if the keys in our map are strings, we can do
something like sum the ASCII codes of the characters in the string.
Generally, we need a (mathematical) function that maps
keys (such as strings) to numbers (that can be used as
array indices).
Such a function is called a hash function,
and an implementation of a map that uses a hash function to
look up a key's value in an array is called a hash table
or hash map,
This is where the name of Java's HashMap class
comes from.
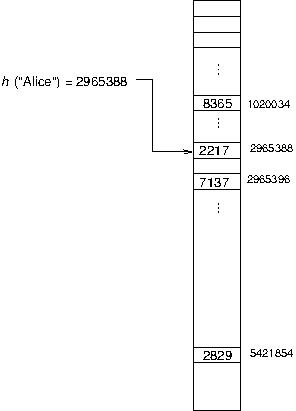
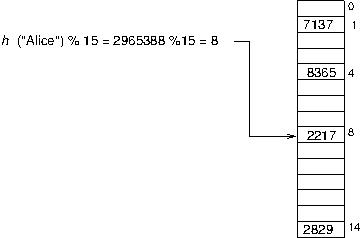
Problem: What if the hash for a key is beyond the bounds of the array? Or, stated another way: it seems like this would require a ginormous (as you kids would put it these days) array. What if we can't afford the space it would take to have an array big enough for all the indices that could be generated for the possible keys? This is no problem at all because with a smaller array we can simply mod (%) the hash by the length of the array, and it will wrap around to a valid array index. Once again, mod makes our life easier.
Problem: What if two keys hash to the same value---that is, what if the hash function assigns the same array index to more than one key? This is a serious problem; we'll refer to this as a collision. In our example above---using the "ASCII sum" of a string as a hash function---any two words that are anagrams of each other (all the same letters, just different order) will collide. Moreover, since we're using mod to map hashes into a smaller array, any two keys whose hashes are the equal when mod'd by the size of the array will collide.
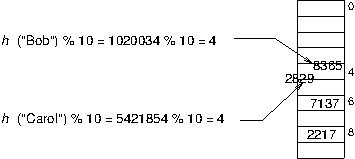
There are several ways to handle collisions. One of the simplest, which we will use here, is called chaining. Instead of assuming an array that holds one value (or one key/value pair) in each position, we'll use an array of pointers to the head of little linked lists of key/value pairs; each linked list (called a bucket) is like the linked list you implemented in Project 3. This is called chaining because the key/value pairs that end up in the same bucket are chained together in the linked list.
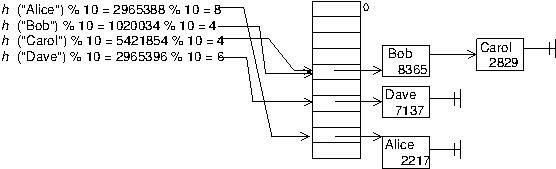
Thus any operation on the map will have two steps. Step 1: find the right bucket by computing the hash of the key, using the hash as an array index. Step 2: find the right node in the chain for that bucket.
Problem: What if all the keys---or even just a lot of them---get hashed to the same bucket? Wouldn't you have a very long chain to search through and we'd be back to O(n) time to look something up? Potentially, yes, that would ruin everything. The trick to avoid that situation is to make the array big enough and the hash function good enough to minimize collisions and prevent any chain from getting too long. It turns out the "ASCII sum" approach is not a very good hash function, but it will do for our purposes, since it's easy to implement.
(The mathy details: if the length of the array is proportional to n (the number of pairs stored) and if the hash function distributes the keys uniformly and independently over the range of array indices, then we can expect constant time for all the operations.)
If at some point the table becomes too full or any one chain becomes too long, then we can rehash the table: make a bigger array and redistribute the keys.
Your task is to implement a hashtable in C.