Lab 10: Heaps and priority queues

The goal of this lab is to learn the specification, implementation, and uses of the priority queue abstract data type.

1. Introduction

A priority queue as an abstract data type is a collection of uniform elements that are comparable (or have some attribute which is comparable), with the operations

• to test if it is empty,
• to test if it is full,
• to insert a new element, and
• to retrieve (and remove) the greatest element, according to how the elements are compared.

Thus priority queues are similar to stacks and queues in that you can add and remove elements in only one way, but they differ in that the order in which elements are removed does not depend on the order in which they were added but instead on some inherent priority.

There are many possible ways to implement a priority queue, but the classical, efficient implementation uses a concrete data structure called a heap. A heap is a variation on a binary tree. Specifically, a heap is a binary tree such that

• it is implemented as an array, using the trick we learned in class for computing the parent, left child, and right child or an element using the element's index.
• it is almost complete, meaning it is complete except possibly in the last level, in which it is filled from the left up to some point.
• it satisfies the heap property, which states that for every node, its comparable attribute is greater than that of either of its children and that the subtrees rooted at its children also satisfy the heap property.

Notice that this specification of a heap gives information both on its abstract/logical structure (being an almost complete binary tree, satisfying the heap property) and its implementation (an array). That is why a heap is a concrete data type; we will use it to implement the abstract data type priority queue.

(Technically, this specifies a max-heap. A min-heap works the same way except the smaller numbers are at the top.)

The following is an example of a heap, viewed both logically and as an array.

The heap will grow and shrink during the running of the programs in which we use it. Since the array cannot grow or shrink, the size of the array will represent a maximum size of the heap, and the portion of the array which it will take up will change. Since we will maintain the property that the the binary tree is almost complete, it will always take up a contiguous portion of the array starting from the beginning; that is, any unused portion of the array will be at the end.

2. Setup

I am providing a bunch of code for you. Copy all the files from the lab11 subdirectory in the course public directory.

cp /cslab/class/cs245/lab10/* .

3. The Heap class

The abstract class Heap contains the basic functionality for a heap that you will extend to make a priority queue. It already has an internal array as an instance variable (plus a heapSize variable that tells how much of the array is in use) and helper methods to calculate the children and parent from a given index. (The math for calculating children and parents is a little different to make up for the fact that we do not have an unused position at 0.)

What you need to provide for the heap is the implementation for a helper method heapify(), which we call on a heap given a node identified by its index. heapify() enforces the heap property on the tree rooted at the given index--- under certain assumptions. This method can be used to set up the array so that it satisfies the heap property, or it can be used to fix up the heap if some other operations result in a violation of the heap property.

This method assumes that both subtrees of the given node satisfy the heap property (the are greater than their children, etc), but the given node might violate it; it might be smaller than one of its children. heapify() fixes up the subtree rooted at the given node by pushing it down until there no longer is a violation. The following illustrates the process needed to fix up the heap if 19 were replaced with 10.

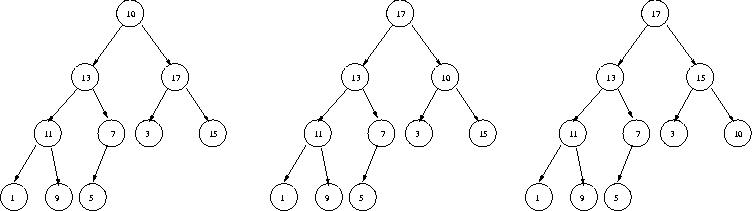
Study this example and figure out what's going on.

Write this method and compile. The file Test.java contains a program to test your work as you go along, but it does not contain anything to test heapify() by itself; you will test it along with the next section.

4. Excursus: Heapsort

Before we implement priority queues, we'll explore a bonus application of heaps: A nifty and very efficient sorting algorithm, called heapsort.

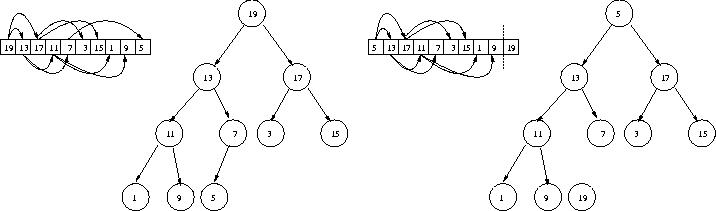
Now 19 is correctly placed in the array, but we no longer have a heap because 5 is in violation. So we call heapify() with the root to fix up the violation incurred. We repeat this whole process (swapping the root with the last leaf, then heapifying) until the heap is "empty"-- although the array is still full, just none of it is counted as part of the heap.

The method sort() in class HeapSorter is static, but it instantiates subclass HeapSorter of Heap to store its data. Complete the constructor of this class so that it initially converts an array into a heap (using repeated and strategic calls to heapify()--- think about this carefully) and write the code for the sort() method, using the strategy described above.

Then test your work using the Test program. Open it to see how it works. By running

java Test heapsort

it will sort an array and print out the sorted version.

5. Class PriorityQueue

Now we will implement the priority queue class. This also is an extension of the Heap class. The isEmpty(), isFull(), and max() methods are easy and already completed for you. What remains is code for adding and removing elements.

First, adding an element. Our strategy is simply to place it in the next available position in the array and increment the size of the heap. This may result in a violation of the heap property--the new element may be larger than its parent. If that happens, then we move the new element up the tree until it is in an appropriate place. Consider the following illustration of adding the element 16:

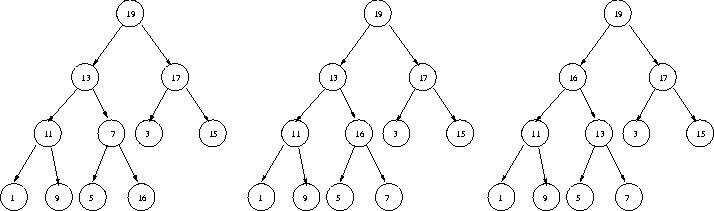
Next, removing the maximum element. Our strategy is to copy the last element in the heap to the first position in the array and then decrease the size of the heap, as illustrated here.

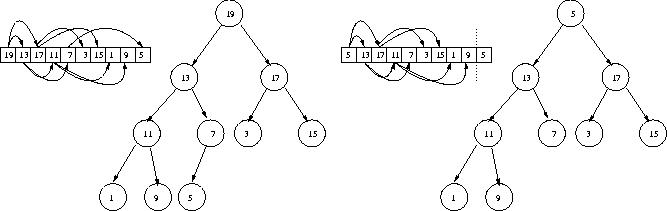
Then use heapify() to correct the violation incurred.

Implement these two methods, then test it using java Test pq.

6. Using a priority queue to implement a queue

To take us back around to stacks and queues, consider how a priority queue can be used to implement a queue: As each element is entered into the priority queue, it is assigned a priority based on its time of arrival. This implies that the element is distinct from its priority---different from the examples we've seen so far where the element is an integer which is used as its priority.

To get around this, the class Queue has two instance variables--- a PriorityQueue and a HashMap. The HashMap associates priorities with elements, and the PriorityQueue stores priorities.

Consider this scenario. An element, say 3, is entered into the queue. It is assigned a priority 15. Thus we insert 15 into the PriorityQueue and associate 15 with 3 in the HashMap. Sometime later, removeFront() is called on the Queue, which in turn calls extractMax() on the PriorityQueue, which returns 15. We then lookup 15 in the HashMap and find 3; 3 then is the value returned from removeFront().

The real trick to all this is determining how to assign priorities.

Implement what's left in the Queue class, and test it using java Test queue.

7. Using a priority queue to implement a stack

Finally, do the same thing as in the previous section, but implement a stack. The only real difference is how you assign priorities. Test using java Test stack.

8. Turn in

Turn in a script showing your code and the result of running each test.