Lab 9: Heaps and priority queues

The goal of this lab is to learn the specification, implementation, and uses of the priority queue abstract data type.

A priority queue as an abstract data type is a collection of uniform elements that are comparable (or have some attribute which is comparable), with the operations

• to test if it is empty,
• to test if it is full,
• to insert a new element, and
• to retrieve (and remove) the greatest element, according to how the elements are compared.

Thus priority queues are similar to stacks and queues in that you can add and remove elements in only one way, but they differ in that the order in which elements are removed does not depend on the order in which they were added but instead on some inherent priority.

There are many possible ways to implement a priority queue, but the classical, efficient implementation uses a concrete data structure called a heap. A heap is a variation on a binary tree. Specifically, a heap is a binary tree such that

• it is implemented as an array, using the trick we learned in class for computing the parent, left child, and right child or an element using the element's index.
• it is almost complete, meaning it is complete except possibly in the last level, in which it is filled from the left up to some point.
• it satisfies the heap property, which states that for every node, its comparable attribute is greater than that of either of its children and that the subtrees rooted at its children also satisfy the heap property.

Notice that this specification of a heap gives information both on its abstract/logical structure (being an almost complete binary tree, satisfying the heap property) and its implementation (an array). That is why a heap is a concrete data type; we will use it to implement the abstract data type priority queue.

(Technically, this specifies a max-heap. A min-heap works the same way except the smaller numbers are at the top.)

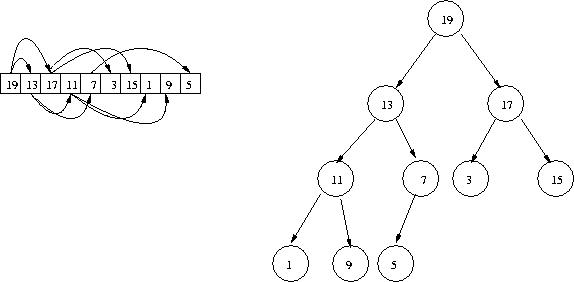
The following is an example of a heap, viewed both logically and as an array.

The heap will grow and shrink during the running of the programs in which we use it. Since the array cannot grow or shrink, the size of the array will represent a maximum size of the heap, and the portion of the array which it will take up will change. Since we will maintain the property that the the binary tree is almost complete, it will always take up a contiguous portion of the array starting from the beginning; that is, any unused portion of the array will be at the end.

I will be providing you with a partially-written class called Heap which you will use to build a PriorityQueue class. (Specifically, Heap will be an abstract class and the PriorityQueue class will extend it.

Your first task in lab will be to write a method in Heap called heapify(), which we call on a heap given a node identified by its index. heapify() enforces the heap property on the tree rooted at the given index--- under certain assumptions. This method can be used to set up the array so that it satisfies the heap property, or it can be used to fix up the heap if some other operations result in a violation of the heap property.

This method assumes that both subtrees of the given node satisfy the heap property (the are greater than their children, etc), but the given node might violate it; it might be smaller than one of its children. heapify() fixes up the subtree rooted at the given node by pushing it down until there no longer is a violation. The following illustrates the process needed to fix up the heap if 19 were replaced with 10.

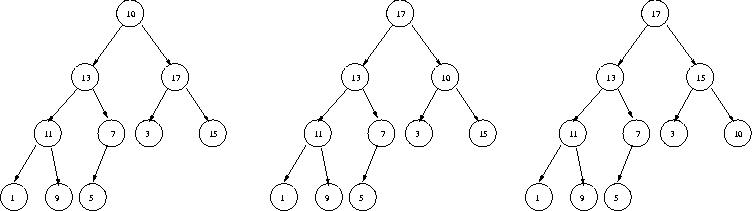
Study this example and figure out what's going on.