The purpose of these practice problems is to simulate the experience of taking the programming portion of Test 3 by providing exemplary problems. The set-up for Test 3 will be similar to that of Test 2: you will be given an Eclipse window and a local copy of the Java API. Internet connectivity will be turned off. Accordingly, you are strongly advised not to look at any resource besides the Java API when taking these practice problems. (I do not anticipate you really needing the Java API, but it will be there "just in case.")
Remember that in the real Test 3 you will not be given a full set of JUnit tests.
Get the starter code from
~tvandrun/Public/cs345/test3-practice
and set it up as you would for a project.
The code is organized into one package per problem
(not in the adt/impl etc
packages as in the projects).
You are playing a computer game in which the hero must pass through a hallway collecting treasure. The hallway is divided into n segments, and on each segment there is a treasure on the left side of the hall and on the right side of the hall. At each step the hero mush be on one side of the hall, ie, on the left side or the right side, and can pick up only the treasure on that side of the hall. There are also n-1 guardians, one between each pair of segments. The guardians charge a fee for crossing to the other side of the hall (ie, left-to-right or right-to-left) when moving to the next segment.
For example, consider this map of the hallway with the value of treasures on the sides and the fees charged by the guardians in the middle:
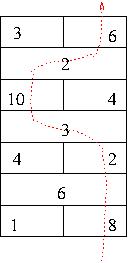
In the pathway shown, the hero started on the right side of the hall. He collected 8 units in segment 0, then two units in segment 1 (still on the right). Then he crossed to the left between segment 1 and 2, having to pay the guardian 3 units. He collected 10 units on the left side of segment 2, crossed again (forfeiting 2 units) and collected 6 units on the right side of segment 3. The net value of treasure gained was 8 + 2 - 3 + 10 -2 + 6 = 21. (This also happens to be the route through this hallway that maximizes the value of the treasure.)
Given the map of such a hallway as an array of left-side treasure,
and array of right-side treasure, and an array of guardian fees,
compute the value of the best route through the hallway.
Complete the body of the method
q1dynprog.HeroHall.bestTreasure().
Test using q1dynprog.HHTest.
(On the final exam you will be given a recursive characterization for the problem. I will also send one for this problem by email, but you should try to characterize it on your own.)
A subsequence of a sequence is a sequence drawn from items in the original sequence in the same order, but not necessarily contiguous. For example, in the sequence "1 2 3 4 5 6 7 8 9 10", the sequence "1 4 5 9" is a subsequence.
A sequence (of integers) is increasing if each number is greater than the number that came before. For example, in the sequence
7 15 13 8 3 11 2 0 14 5 12 4 17
the sequence "7 15 17" is an increasing subsequence. However, the sequence "7 8 11 14 17" is a longer (and, in fact, the longest) increasing subsequence.
Given a sequence of integers as an array,
find the length of the longest increasing subsequence.
Complete the body of the method
q2dynprog.LongestIncreasingSubsequence.longIncrSubsq(),
and test using q2dynprog.TestLIS.
(As with the previous problem, I will send the recursive characteristic by
email, but you should try to derive it on your own.
Hint: I found it useful to think in terms of the slightly-different problem,
"For each position i, find the length of the longest subsequence starting
with and including the value at position i.
We can use the idea behind perfect hashing to
implement a perfect hash set.
If we assume that no call to any set operation will be
made with any key not given to the constructor, we do not need
to store the keys at all (such as in a keys array).
Instead of making each bucket a secondary hash map, as in the project, we can make each bucket to be a bit vector, with each key that would hash to that bucket associated with a bit that indicates whether it is currently in the set or not. Each bucket would have its own secondary hash function, as before; the secondary hash functions would hash to the range Zμ where μ is the number of bits in each bit vector.
Since the short type has size 16 bits, we could make our
buckets array to be of type short[] and
we would need a primary hash function
that hashes no more than 4 keys to each bucket (since 4^2 = 16).
Complete the constructor for such a class as found in
q3hashing.PerfHashBVSet.java.
Specifically, fill in ``PART A'' and ``PART B'' such that
an appropriate primary hash function (no more than four collisions per bucket)
and appropriate secondary hash functions (no collisions in-bucket)
are found.
Test using q3hashing.TestPHBVS.
(If this sounds scary, take a deep breath and give it a try. If you remember the perfect hashing project, then this actually isn't too much of a reach (as long as you remember bit vectors also). This problem appeared on a real test Spring 2015 and the students did quite well.)
Recall that the performance of a hashtable using open-addressing depends on the number of probes needed to find a key (or determine that the key does not exist), which in turn depends on the length of the cluster the key is in (or would be).
Consider the reduced version of an open-addressing-with-linear-probing
hashmap implemented as q4hashing.LinProbHashMap.
It has one extra operation, a method to compute the average
cluster length.
For example, if we were visualize a hashtable as an array with
. indicating empty positions and #
indicating filled positions, then the following hashtable
[..#.####.....#...###...#.....#######....##..]
has 7 clusters with a total of 19 items over all clusters and thus an average cluster length of 2.7142857.
Implement the method
q4hashing.LinProbHashMap.aveClusterSize().
Test using q4hashing.TestLPHMAveCluster.
Recall that the quicksort algorithm works by selecting a pivot element from an array (for example, the last element), partitioning the array into a section of elements less than the pivot and a section greater than the pivot, putting the pivot itself between the two sections, and then sorting recursively on the two sections.
The quicksort algorithm can be adapted to be used efficiently on an array of strings by picking a pivot (again, for example, the last element) and then partitioning the array into three sections: one for those strings whose first character comes before the first character of the pivot, one for those whose first character is equal to the pivot's, and one for those whose first character comes after the pivot's. For example:

Then we recursively sort all three sections except that in the middle section we then sort on the second character, etc.
Finish the implementation of string quick sort
found in d5string.QuickSortString.quicksortStringR().
Note that this method has a parameter c that is used
to indicate the size of the prefix assumed to be identical on all
strings in the range.
In the example above, the recursive call of quicksort on the
portion equal to the pivot would have c as 1.
The method q5string.QuickSortString.quicksort()
takes only the array of Strings and makes the top-level call to
quicksortR().
Test using d5string.QSSTest.
If this question appeared in the real test (as it did Spring 2015),
you would be allowed to assume all strings have the same length,
and the test testTLWs() exercises this method under that
assumption.
For a bigger challenge, make no such assumption;
the test testNames() exercises the method
with strings of varying lengths.