[The following talks about "three projects." Only the first two of the three are assigned projects to be turned in. The third (one left-leaning red-black trees) is recommended for practice, but does not need to be turned in.]
The goal of these next three projects (AVL trees, traditional red-black trees, and left-learning red-black trees) Is to understand how these three balanced binary search tree strategies work by implementing them. The three projects will use the same code base, and in some ways can be seen as a single, big project. Splitting them up into three projects, however, will help you spread out the work on them; for example, you are encouraged to start work on the AVL tree project (described here) after we learn AVL trees rather than waiting until we learn all the varieties of trees.
One part that is missing from this series of projects is an experimental section. I haven't developed that part enough yet. You are encouraged to write experiments to compare the running time for your own learning. (Caution: you'll probably find that you need fairly large amounts of data to see the effects.)
As mentioned before, the code base is the same for all three
projects,
and this section will give an overview of the whole code.
Copy the given code from ~tvandrun/Public/cs345/bal-tree
and make an Eclipse project for it.
As usual, you will find adt, impl,
and test packages.
The most important part of the adt package is
the Map interface, which has a slight modification
from the previous versions we've seen: the remove()
method signature has (ironically) been removed.
Because the various kinds of balanced BSTs have a fair amount of code in common, we have a complicated type heirarchy:
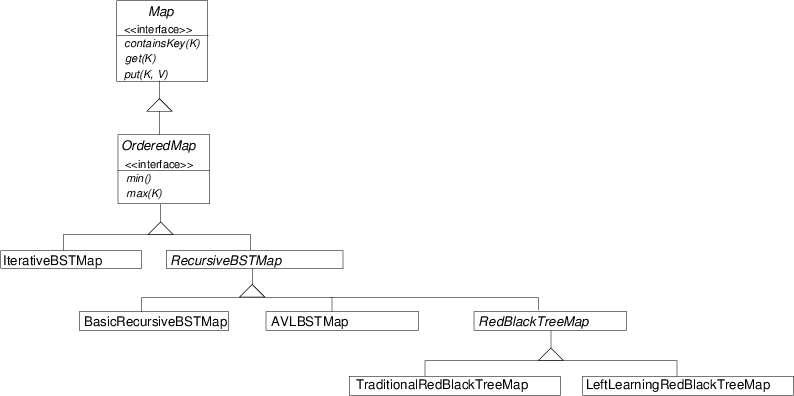
IterativeBSTMap does not share any code
with the other types, since it takes a completely different approach.
In fact, it's not even included with the given code of this project,
though we have seen it in class.
The abstract class RecursiveBSTMap contains all
the code for manipulating a binary search tree except for anything
that would verify that the tree meets the properties of various
balancing strategies and any code that would fix up a tree that is
out of balance.
That is deferred to the child classes.
The child class BasicRecursiveBSTMap implements
verification and fixup by... doing nothing.
RecursiveBSTMap also has a strategy object
for verification.
The verification strategies have their own class heirarchy (not shown),
where there is a verification strategy class for each of AVL trees,
traditional RB trees, and left-leaning RB trees.
Don't modify classes like AVLVerify.
You won't be turning them in.
The idea is to keep you from (accidentally or dishonestly)
changing the verification code so that it allows things that
aren't really AVL trees or RB trees.
The classes AVLBSTMap, TraditionalRedBlackTreeMap,
and LeftLeaningRedBlackTreeMap each provide the fix-up code---or
they will, once you finish them, since that is your task
in the three projects.
However, since the interesting code for these classes (including the fix-up code you need to write) are implemented recursively in the nodes, the type hierarchy for nodes is just as important and even more complicated. Here it is, but not showing the red-black tree node classes (to simplify it a bit):
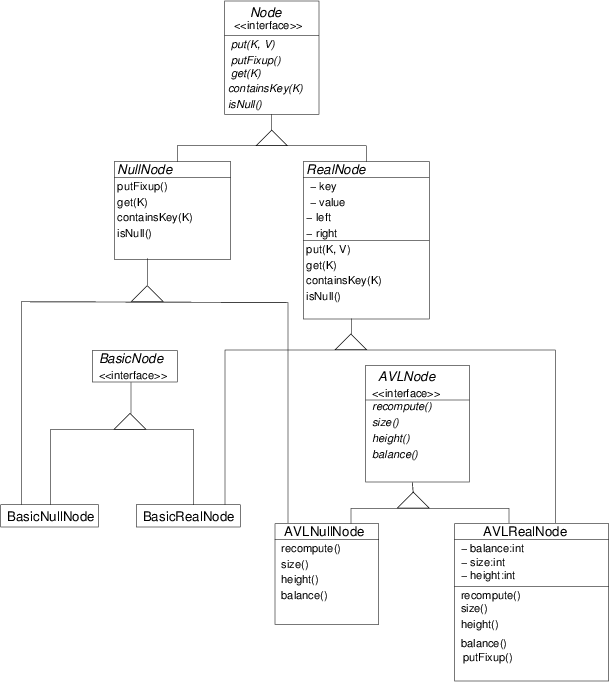
This mainly mirrors the type hierarchy for the tree classes, but with another dimension: The trees are not going to have acutal null references, since that would require extra checks every time we use a link. Instead, "null" links will be references to special objects called null nodes. The advantage is that these objects can respond to the same methods as real nodes. Hence for every kind of tree, we have both a null node class and a "real" node class.
Take some time to understand how RecursiveBSTMap
and its node classes
are set up and how their code works.
Notice how NullNode implements operations trivially.
An important method signature in
Node
is putFixup().
Most of your work in each of these three projects will
be writing implementations for this in the "real node" classes, to rebalance the
tree when it is in violation of the balance properties.
Turn your attention to AVLBSTMap.
The interface AVLNode defines some
additional operations for the nodes of AVL trees.
AVL tree nodes will store information about the size, height,
and balance of the subtree rooted at that node.
Note that "balance" is defined as an integer which is
the left height minus the right height.
Thus if the subtrees have the same height, balance is zero.
That doesn't mean the subtee is perfectly balanced, since the
left and right subtrees might themselves be off balance.
But it means that there is no problem with respect to each other.
These attributes could be computed on demand, recursively.
However, that would require traversing the whole (sub-)tree,
which would kill performance---it would defeat the purpose
of using binary search trees.
So instead we store that pre-computed information in the nodes.
However, that information could become out of date when an
insertion is made or when the tree rotates.
We'll need to recompute those values.
But even then, we don't want to traverse the whole tree;
we recompute a node's height, size, and balance by
assuming the node's children's values are correct
and recomputing based on those values
(for example, subtracting the children's heights to get a new balance value).
This is done by recompute().
It is the responsibility of the code you write in putFixup()
to balance and recompute as necessary.
When the code is verified, the verification strategy will
throw an ImbalanceException if the AVL
property is violated.
It will throw an IgnorantNodeException if
a node has incorrectly stored height.
Write the body of AVLBSTMap.AVLRealNode.putFixup().
This is a hard task; my solution took around 60 lines of code,
and there's no other way to do this than work through the details
of the various cases.
Here's a way to organize it:
replacement is initialized to this.
Other hints:
oldRight and
oldLeftRight to keep track of nodes in relation to
this while doing rotations.
assert.
If you think something has to be a certain way (balance is in or
outside a certain range, a node has to have a certain type), then
assert it.
AVLNode, which
means the objects they refer to could be AVLNullNode.
This makes a difference because you'll need to get at a
node's left and right, but
AVLNullNode doesn't have them.
If you think you need to get a node's left
and right, then you better be sure it is not null.
In that case, cast it.
Make a new variable of the type AVLRealNode,
and then you can get at its left and right.
For example:
RealNode oldLeft = (AVLRealNode) left;
AVLRealNode oldLeftRight = (AVLRealNode) (oldLeft.right);
Make sure you understand how casting works!
This doesn't change any node object to be a different type, and
this doesn't make any new objects.
This merely asserts that left is
an AVLRealNode and uses it as such.
This won't work (ie, it will throw a ClassCastException)
if the object left refers to is not
an instance of a subtype of AVLRealNode.
Test using AVLBSTMTest.
Copy the file you modified (AVLBSTMap)
to your turn-in folder /cslab/class/cs345/(your id)/avl .
To keep up with the course, this should be finished by March 17.