Project: Heaps and priority queues

With the jawbone of a donkey
heaps upon heaps,
with the jawbone of a donkey
have I struck down a thousand men.

Judges 15:16

1. Introduction

The goal of this project is to learn the specification, implementation, and uses of the priority queue abstract data type. If this project feels like a Programming II lab, it's because it was at one time a Programming II lab, one of my favorites, that had to get cut for the sake of time. But it now has new life as a DS&A project.

The project accompanies the material found in Section 2.3 in the book, but there isn't any project in the book for it (yet). Moreover, Section 2.3 in the draft printed at the bookstore is out of date in at some points. The main difference is that the method called heapify() in the text is called sinkKeyAt() in the revised version of the code, and there is a corresponding raiseKeyAt().

A priority queue as an abstract data type is a collection of uniform elements that are comparable (or have some attribute which is comparable), with the operations

• to test if it is empty,
• to test if it is full,
• to insert a new element, and
• to retrieve and/or remove the greatest element, according to how the elements are compared,
• to test whether an element is in the collection,
• to indicate that an element's priority has increased.

Thus priority queues are similar to stacks and queues in that you can add and remove elements in only one way, but they differ in that the order in which elements are removed does not depend on the order in which they were added but instead on some inherent priority.

The elements will be referred to as keys to be consistent with the terminology used for sets and maps. The last operation listed above, "increase key," is a more specialized operation which may seem out of place in this project, but it will prove useful later in the course with some algorithms that use efficient priority queues.

There are many possible ways to implement a priority queue: One could imagine a list or set where one simply searches for the highest priority key, or we could maintain a list sorted by the keys' prioirties. The classical, efficient implementation, however, uses a concrete data structure called a heap. A heap is a variation on a binary tree. Specifically, a heap is a binary tree such that

• it is implemented as an array, where a node's children are stored in positions that can be calcuated from the position of the node itself, essentially by doubling the node's index.
• it is almost complete, meaning it is complete except possibly in the last level, in which it is filled from the left up to some point.
• it satisfies the heap property, which states that for every node, its comparable attribute is greater than that of either of its children and that the subtrees rooted at its children also satisfy the heap property.

Notice that this specification of a heap gives information both on its abstract/logical structure (being an almost complete binary tree, satisfying the heap property) and its implementation (an array). That is why a heap is a concrete data type; we will use it to implement the abstract data type priority queue.

(Technically, this specifies a max-heap. A min-heap works the same way except the smaller numbers are at the top.)

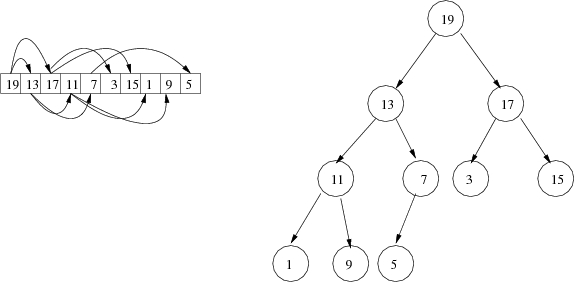
The following is an example of a heap, viewed both logically and as an array.

The heap will grow and shrink during the running of the programs in which we use it. Since the array cannot grow or shrink, the size of the array will represent a maximum size of the heap; as the heap grows and shrinks it will take up a larger or smaller portion of the array. Since we will maintain the property that the the binary tree is almost complete, it will always take up a contiguous portion of the array starting from the beginning; that is, any unused portion of the array will be at the end.

I am providing you with a partially-written class called Heap which you will use to build a priority queue. Specifically, PriorityQueue is an interface specifying the operations of any priority queue, not just one implemented using a heap; Heap is an abstract class giving the basic implementation of the heap data structure; and HeapPriorityQueue extends the Heap class and implements PriorityQueue.

Your first task in this project will be to write a method in Heap called sinkKeyAt(), so called because it is used to indicate that the key stored at a given index may be in the wrong position, specifically that it may be too small and needs to "sink" down to the right position in the heap. Some sources refer to this operation as heapify, since it enforces the heap property on the subtree rooted at the given index. That is the postcondition of this method: the subtree rooted at that index is a valid heap. It is a step in building a heap.

The precondition of this method is that both child subtrees of given position are already heaps. In other words, the tree rooted at the given index has the heap property except that the key at the root of the subtree (the key at the given position) may violate it. We check this at the beginning of the method by calling the verification method isHeapBut(), which returns true if the two child subtrees of the given position are heaps.

sinkKeyAt() fixes up the subtree rooted at the given node by pushing it down until there no longer is a violation. The following illustrates the process needed to fix up the heap if 19 were replaced with 10.

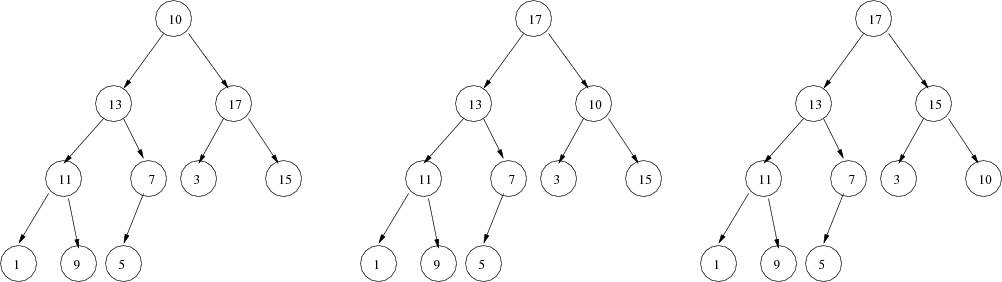
Study this example and figure out what's going on. Note that this method makes no assumptions, before or after, about the state of the rest of the heap, either positions higher in the tree or on different branches.

2. Setup

Copy the give code from ~tvandrun/Public/cs345/heap and make an Eclipse project for it. You will find three packages: adt for interfaces specifying abstract data types, impl for the classes you will write or finish to implement the abstract data types, test for the JUnit tests, and exper for an experiment to finish the project off. The package impl also contains a program called Test

3. The Heap class

The abstract class Heap contains the basic functionality for a heap that you will extend to make a priority queue. It already has an internal array as an instance variable (plus a heapSize variable that tells how much of the array is in use) and helper methods to calculate the children and parent from a given index.

Since the keys in the heap can be any type, we need to have some way to compare them based on their priority. Thus the class also has a Comparator instance variable compy that is used to determine, given two keys, which has the higher priority. In some of the next parts of this project you will need to write appropriate comparators, but in this part you need only to use the comparator.

What you need to provide for the heap is the implementations for two helper methods: sinkKeyAt(), described above; and raiseKeyAt(), which is the companion to sinkKeyAt(). In raiseKeyAt(), we assume that the entire heap is valid (not just the subtrees) except that the value in the given position, which might be too great and thus should be moved higher in the heap.

One very important thing for these methods: Do not move keys around in the array directly. Instead, interchange keys using the swap() helper method. This is important for an optimization to be made to heap priority queues in future projects.

These operations can be done either recursively or iteratively. You are encouraged to think about it both ways. Write this methods and test it using the JUnit test in test.HeapTest. Once you've done these, the hard part of the project is done.

4. Excursus: Heapsort

Before we implement priority queues, we'll explore a bonus application of heaps: A nifty and very efficient sorting algorithm, called heapsort.

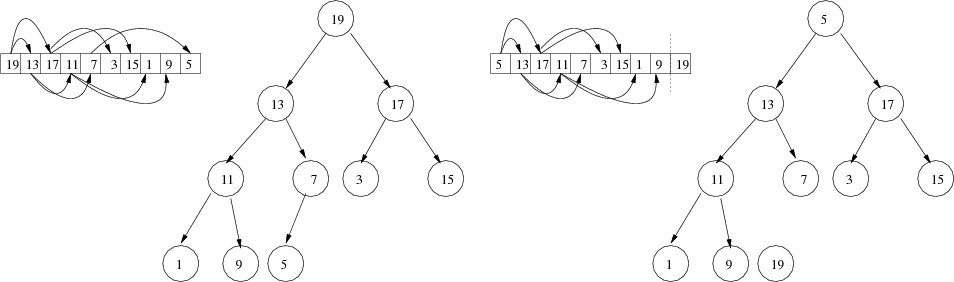
Now 19 is correctly placed in the array, but we no longer have a heap because 5 is in violation. So we call sinkKeyAt() with the root to fix up the violation incurred. We repeat this whole process (swapping the root with the last leaf, then heapifying) until the heap is "empty"-- although the array is still full, it's just that none of it is counted as part of the heap.

The method sort() in class HeapSorter is static, but it instantiates subclass HeapSorter of Heap to store its data. Complete the constructor of this class so that it initially converts an array into a heap (using repeated and strategic calls to sinkKeyAt()--- think about this carefully) and write the code for the sort() method, using the strategy described above. (In the constructor you will also need to make a comparator object that will compare integer keys appropriately. Do this with an anonymous inner class.)

The JUnit testcase test.HeapSortTest will test this.

5. Class HeapPriorityQueue

Now we will implement a priority queue based on a heap. You'll notice that two other implementations of the PriorityQueue interface are given, NaivePriorityQueue and SortedPriorityQueue. Your task is to finish the class HeapPriorityQueue.

This also is an extension of the Heap class. The constructors and the isEmpty(), isFull(), and max() methods are easy and already completed for you. What remains is code for adding and removing elements.

First, adding an element. Our strategy is simply to place it in the next available position in the array and increment the size of the heap. This may result in a violation of the heap property--the new element may be larger than its parent. If that happens, the we fix it using raiseKeyAt(). Consider the following illustration of adding the element 16:

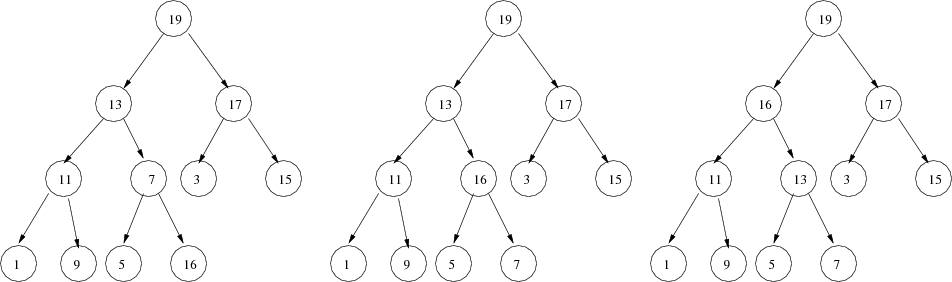
Next, removing the maximum element. Our strategy is to copy the last element in the heap to the first position in the array and then decrease the size of the heap, as illustrated here.

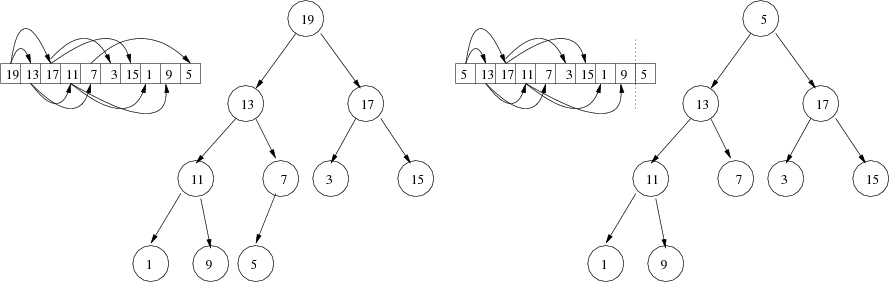
Then use sinkKeyAt() to correct the violation incurred.

Implement these two methods, then test it using test.HPQTest. The tests stressTest and insertPollLots will take a long time.

(Implementations for contains() and increaseKey() are given. You are encouraged to think through these methods.)

6. Using a priority queue to implement a queue

To take us back around to stacks and queues, consider how a priority queue can be used to implement a queue: As each element is entered into the priority queue, it is assigned a priority based on its time of arrival.

The class PQQueue has two instance variables--- a PriorityQueue and a HashMap (from the Java API). The HashMap associates elements in the queue (which are also keys in the priority queue) with integer priorities. We'll give the priority queue a comparator that uses this map to look up a key's priority.

The real trick to all this is determining how to assign priorities and how to write the comparator to determine realtive priorities of keys.

Implement what's left in the PQQueue class, including the constructor. The constructor will need to instantiate the HeapPriorityQueue class, passing a comparator to its constructor. Write this comparator as an anonymous inner class. This this using test.PQQTest.

7. Using a priority queue to implement a stack

Finally, do the same thing as in the previous section, but implement a stack (PQStack). The only real difference is how you calculate priorities. Test using test.PQSTest.

8. Experiment

This last part doesn't require any work from you. You will run an experiment on your code and observe the results.

As mentioned above, a priority queue can be implemented "naively", simply by searching a list for highest-prioritized key, or in a slightly better way by maintaining a list sorted by priority. These approaches are given to you in impl.NaivePriorityQueue and impl.SortedPriorityQueue, respectively.

The program exper.Experiment does a quick experiment to compare the performance among these. Examine and run this program. Make sure that assertion-checking is turned off for the experiments, because the validation itself takes a significant amount of time. What to you observe? (Hint: If HeapPriorityQueue doesn't blow the others out of the water, something's wrong.)

This is not the real way to do performance experiments---rigorous methods would do more to control other variables and would relate how running time grows with how the size of the data grows. But for our present purposes this will do.

9. Turn in

Copy the files you modified (Heap, HeapSorter, HeapPriorityQueue, PQQueue, and PQStack to your turn-in folder /cslab/class/cs345/(your id)/heap .

To keep up with the course, this should be finished by Feb 2.