The purpose of these practice problems is to simulate the experience of taking Test 2 by providing exemplary problems. On Test 2 you will be given an Eclipse window. You will also be able to view a local copy of the Java API. Internet connectivity will be turned off. Accordingly, you are strongly advised not to look at any resource besides the Java API when taking these practice problems.
(In fact, it's unlikely you'll need the Java API for either these practice problems or the test. I will provide implementations of all abstract data types that you would rely on---lists or queues or whatever. Also, Eclipse itself gives contextual help that provides most of the information you would get from the Java API. Access to the Java API is given only "just in case.")
Note that in the real Test 2 you will not be given a full set of JUnit tests.
Get the starter code from
~tvandrun/Public/cs345/test2-practice
and set it up as you would for a project.
The code is organized into one package per problem
(not in the adt/impl etc
packages as in the projects).
You can find solutions to these problems in
~tvandrun/Public/cs345/test2-practice-soln.
Suppose you need an implementation of the Bag ADT for
Strings that supports fast lookup and adding;
"fast" here means logarithmic time.
Further suppose that you know all of the potential keys ahead of time;
that is, when the bag class is instantiated, before you have tallied
any keys, you have a complete list or set of all the Strings
that might be added to the set.
(For example, you are counting word frequencies in a text, but you already
know the full vocabulary in that text.)
Implement the class String; it is not generic.
Specifically, implement it
so that its operations add(), count(),
and remove() operate in O(lg n) time,
where n is the number of potential keys.
Moreover, assume that the potential keys are passed to the
constructor as an Iterator that returns the keys
in sorted order.
(Note that the iterator received by the constructor is different from
the iterator returned by the FastBag.iterator();
the order of the keys returned by the iterator you write is
unspecified, and it should return the keys the number of times
they occur.)
Although this is in the spirit of a test problem, it is a tad longer than an actual test problem would be.
Test using q1sortedArrayBag.TestSABag.
(Hint: The phrases "logarithmic time" and "keys in sorted order" should prompt you to think "binary search.")
Our definition of a heap as an data structure for implementing the priority queue ADT included the idea that the heap would be stored in an array, arranging the nodes in a breadth-first manner, with the root at position 0, its children at positions 1 and 2, etc. Alternately, we could implement the same heap abstraction using a linked tree (it would just be less efficient). That is, the implementation would include a node class, with each node having links to two children. So that we can also ascend the tree (when a key's priority increases), the node will also have a link to its parent.
The class q1adt.LinkedHeapPriorityQueue implements
the heap abstraction with a linked tree.
The nested class ode represents the individual nodes,
each containing a key.
The instance variable root refers to the node containing
the highest priority key.
A helper method swap() takes two nodes and
interchanges their keys.
This is used to for fixing up priority violations
rather than moving nodes around.
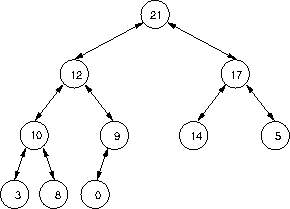
a. Complete the private helper method increaseKeyAt(),
which takes a node at which there might be a violation with a key
being too low for its position and fixes up the tree.
For example, given the node with 21 in the heap below, it would
fix up the heap to what appears in the original example.
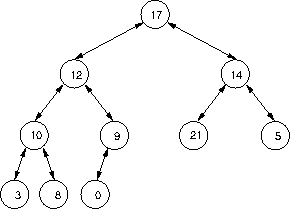
b. Complete the private helper method decreaseKeyAt(),
which takes a node at which there might be a violation with a key
being too high for its position and fixes up the tree.
For example, given the node with 8 in the heap below, it would
fix up the heap to what appears in the original example.
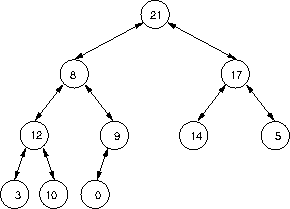
Test using q2linkedHeap.TestLHPQ.
The transpose of a graph is a graph with the same (number of vertices) but with the edges reversed. That is, for graph G = (V, E), the transpose of G is GT = (V, ET) where edge (u, v) is in ET if and only if (v, u) is in E.
Consider the class q3transpose.AdjListGraph which
is exactly as it appeared in the in-class examples and projects from
the graph unit.
Note in particular the nested class ALGBuilder which
is used to build a new AdjListGraph.
Specifically, to build a new graph, use this pattern:
// make the builder AdjListGraph.ALGBuilder builder = new AdjListGraph.ALGBuilder(); // ... add edges using builder.connect(u, v) ... // now that we're done, get the graph AdjListGraph g = builder.getGraph();
Write the method
q3transpose.ComputeTranspose.computeTranspose(),
which takes a AdjListGraph and produces another
AdjListGraph that is the transpose of the
one given.
Test using q5transpose.TestComputeTranspose.
Recall that a cycle is a closed path in a graph, that is, a path that
begins and ends at the same vertex. Consider also the interface
q2graph.Graph which is exactly as it appears in the in-class
examples
and projects that accompanied the graph unit.
Write the method q4checkCycle.CheckCycle.checkCycle()
which takes a Graph
(it
will be an AdjListGraph, but that doesn't matter) and a
starting
vertex
identified by an integer and determines whether there is a cycle of
length at least one beginning and ending with that vertex.
(Equivalently, this determines whether or not there is a cycle that
includes this vertex, since it doesn't matter which vertex in the cycle
is its beginning or ending point.)
If it helps you think about it, you may assume that the graph is directed. (Hint: There are two graph algorithms either of which you could adapt to solve this problem.)
Test using q4checkCylce.TestCheckCycle.
Any binary search tree can be turned into a sorted sequence (or list or array) of keys by doing an in-order depth-first traversal---the keys of the tree would be processed in sorted order and so could be inserted into an array. Likewise we could could turn a sorted array into a BST. If the length of the array were one less than a power of 2, we could turn it into a balanced binary search tree this way:
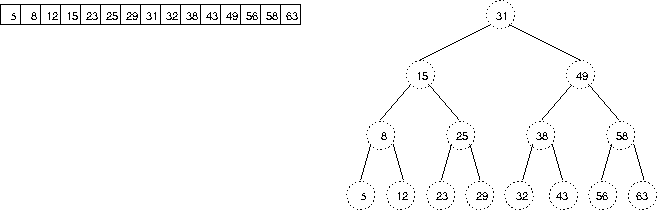
If the length of the array were not one less than a power of 2, we could convert it into one of the varieties of nearly-balanced trees.
Consider the simplified implementation of red-black trees
represented by the class q5array2rb.RBNode.
This represents only the data (keys, links, and redness)---any
operations such as lookup, insertion, and rotations would
need to be implemented externally.
Complete the method q5array2rb.Sorted2RB.sorted2RB()
which takes a sorted array of Strings and returns
an equivalent red-black tree represented by its root,
an instance of RBNode.
For example, given

It could return
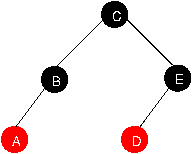
Recursion is recommended.
Specifically, it is recommended that the method
Sorted2RB.sorted2RB() delegate the work to
a recursive helper method.
I'm not giving you a stub or signature for that helper method
because determining appropriate parameters to that helper
method is part of the problem.
Also, in the example above the red-black tree happens to be
left-leaning, and in my own solution the resulting tree
always is a left-leaning red-black tree.
That's not required, though---your solution could produce different trees
from
mine, as long as they are valid red-black trees, valid BSTs, and
contain all and only the given keys.
Test using q5array2rb.TestSTRB
Consider the simplified classes to represent nodes in
red-black trees and two-three trees in the
Finish the two methods in q6llrb1tt.Convert:
llrb2tt(), which takes an
RBNode as
the root of a left-leaning red-black tree and converts
that tree into a two-three tree and returns the root
TwoThreeNode;
and tt2llrb() which takes a
TwoThreeNode as the root
of
a two-three tree and converts that tree into a left-leaning red-black
tree
and returns the root RBNode.
You may assume the trees passed into the methods are valid left-leaning red-black trees or two-three trees---that is, you do not need to check or verify anything about them. Recursion is recommended.
Test using q6llrb2tt.TestConvert.