The purpose of these practice problems is to simulate the experience of taking the programming portion of Test 4 by providing exemplary problems. The set-up for Test 4 will be similar to that of Test 2: you will be given an Eclipse window and a local copy of the Java API. Internet connectivity will be turned off. Accordingly, you are strongly advised not to look at any resource besides the Java API when taking these practice problems. (I do not anticipate you really needing the Java API, but it will be there "just in case.")
Remember that in the real Test 4 you will not be given a full set of JUnit tests.
Get the starter code from
~tvandrun/Public/cs345/test4-practice
and set it up as you would for a project.
The code is organized into one package per problem
(not in the adt/impl etc
packages as in the projects).
(On the final exam you will be given a recursive characterization for dynamic programming problem problem. For the practice ones below (#1 and #2), you can find recursive characterizations here, though I encourage you to characterize them on your own before---or instead of---looking.)
You are playing a computer game in which the hero must pass through a hallway collecting treasure. The hallway is divided into n segments, and on each segment there is a treasure on the left side of the hall and on the right side of the hall. At each step the hero mush be on one side of the hall, ie, on the left side or the right side, and can pick up only the treasure on that side of the hall. There are also n-1 guardians, one between each pair of segments. The guardians charge a fee for crossing to the other side of the hall (ie, left-to-right or right-to-left) when moving to the next segment.
For example, consider this map of the hallway with the value of treasures on the sides and the fees charged by the guardians in the middle:
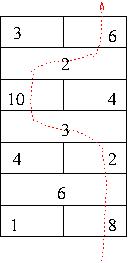
In the pathway shown, the hero started on the right side of the hall. He collected 8 units in segment 0, then two units in segment 1 (still on the right). Then he crossed to the left between segment 1 and 2, having to pay the guardian 3 units. He collected 10 units on the left side of segment 2, crossed again (forfeiting 2 units) and collected 6 units on the right side of segment 3. The net value of treasure gained was 8 + 2 - 3 + 10 -2 + 6 = 21. (This also happens to be the route through this hallway that maximizes the value of the treasure.)
Given the map of such a hallway as an array of left-side treasure,
and array of right-side treasure, and an array of guardian fees,
compute the value of the best route through the hallway.
Complete the body of the method
q1heroHall.HeroHall.bestTreasure().
Test using q1heroHall.HHTest.
Recall that in the far-off country of Micomicona all streets are one-way. Most cities are laid out as a grid with each horizontal road segment being one-way eastbound and each vertical road segment being one-way northbound, with one extra road taking one from the northeast corner of the city back to the southwest corner, such as in this city:
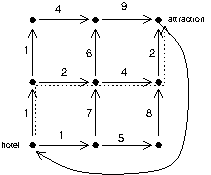
Typically, as in the city shown, there is a hotel in the southwest corner of a city and a tourist attraction at the northeast corner. The tourism board monitors the traffic in each road segment. The travel time in minutes for each segment (for some point it time) is shown. They want to provide an app for tourists that helps them find the fastest route from the hotel to the attraction. In this case the fastest route (shown dotted) takes 9 minutes.
(The road from the attraction back to the hotel doesn’t play into this problem.)
Let n and m be the dimensions of the city’s grid, that is, n is the number of intersections from west to east and m is the number of intersections from south to north. Let the southwest corner be intersection (0, 0) and the northeast corner be intersection (n − 1, m − 1).
Use dynamic programming to finish the method
q1onewayGPS.OneWayGPS.getBestTravelTime()
which takes the dimensions of the city and arrays indicating the travel times for the
east-bound and north-bound segments and returns the minimum travel time from
the southwest corner to the northeast corner.
Test using q1onewayGPS.OWGPSTest.
We can take ideas from the separate chaining, open-addressing-with- linear-probing, and perfect hashing to make a hybrid approach to building a hash table: Like perfect hashing, there will be both a primary table and secondary tables. Like separate chaining, the primary table will be an array of buckets, and the key’s hash will determine which bucket the key goes in. Unlike separate chaining, the buckets will be secondary tables (instead of linked lists), and unlike perfect hashing there will be collisions in the secondary tables, which will be handled by linear probing. In short, this approach is like separate chaining but with linear-probe tables as buckets.
Class q3hybridHash.HybridHashSet
implements a simplified hash table using the ap-
proach. The simplifications are (a) it is a set, not a map; (b) it is not generic, but
specifically for strings; (c) there is no support for removal; (d) there is no support for
iteration (although that would have made for an awesome test problem) (e) there
is no support for resizing/rehashing (we simply “hope” that the table will never
be too full). The nested class Bucket implements a linear-probing open-addressing
hashtable as the buckets/secondary tables.
Complete this class by implementing the following methods:
Test using q3hybridHash.HHTest.
We can use the idea behind perfect hashing to
implement a perfect hash set.
If we assume that no call to any set operation will be
made with any key not given to the constructor, we do not need
to store the keys at all (such as in a keys array).
Instead of making each bucket a secondary hash map, as in the project, we can make each bucket to be a bit vector, with each key that would hash to that bucket associated with a bit that indicates whether it is currently in the set or not. Each bucket would have its own secondary hash function, as before; the secondary hash functions would hash to the range Zμ where μ is the number of bits in each bit vector.
Since the short type has size 16 bits, we could make our
buckets array to be of type short[] and
we would need a primary hash function
that hashes no more than 4 keys to each bucket (since 4^2 = 16).
Complete the constructor for such a class as found in
q3hashing.PerfHashBVSet.java.
Specifically, fill in ``PART A'' and ``PART B'' such that
an appropriate primary hash function (no more than four collisions per bucket)
and appropriate secondary hash functions (no collisions in-bucket)
are found.
Test using q3hashing.TestPHBVS.
(If this sounds scary, take a deep breath and give it a try. If you remember the perfect hashing project, then this actually isn't too much of a reach (as long as you remember bit vectors also). This problem appeared on a real test Spring 2015 and the students did quite well.)
The code in package q5trieIt contains a
class TrieSet similar to the one in the project.
Your task in this problem is to write an iterator for it.
A similar problem appeared as a bonus for the trie project, but that one
was set up to have you write a recursive iterator-of-iterators, as
in the perfect hash map project.
In this case, the iterator method is set up not to be recursive
in the nodes, but intead to be a single iterator in the TriSet
class.
But since this iterator essentially does depth first search over the trie,
you'll need a stack of nodes to keep track of where you've been,
and also keep track of a prefix for the place you currently are in the tree.
Complete the next() method
in the anonymous iterator returned by q5trieIt.TrieSet.iterator().
Test using q5trieIt.TrieItTest.
(This problem is essentially the same as part f of the trie project. It's still useful as a practice problem in that it helps you think through how a problem like this looks as a stand-alone problem such as would appear on the test.)
Consider the reduced form of the class q6trie2array.TrieSet
provided. Specifically
it has only a contains() method and no separate TrieNode class.
Instead of internal
nodes, a TrieSet is itself a node, having other TrieSets as children.
Consider the problem of converting a set implemented as a trie into a sorted array of its keys. For example, the following trie
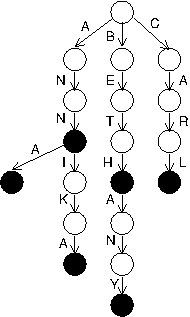
would produce the array {ANN, ANNA, ANNIKA, BETH, BETHANY, CARL }.
This can be done recursively if the method is given the array to be filled (the code calling the method would create a big enough array to begin with), a starting position in the array (indicating how much of the array has already been filled with keys that come before the keys in the current subtrie), and a prefix for the keys in the subtrie (indicating the characters on the path to this subtrie), as in this method signature:
int trie2Array(String[] keys, int start, String prefix)
For example, for the node in the trie above with incoming link labeled T, the method would be called with start having value 3 (because the strings ANN, ANNA, and ANNIKA have already been put in the array) and prefix having value BET (because all the keys in that subtrie begin with BET).
Write the method q6trie2Array.TrieSet.trie2Array(),
which populates the keys array and returns the number of keys
added to the array by that subtrie.
Test using q6trie2Array.T2ATest.