Daily Sep 14. Read Sec 7.(1-3); do 7.1.(2-4) and 7.2.(3&4)
Daily Sep 17.
Read Sec 8.(1-4); do 8.1-(1,3,4).
Section 8.1 is the main thing we'll be looking at;
read it carefully.
Sections 8.(2-4) should be review.
Judge for yourself how carefully to read it---but
you should know the stuff.
HW Sep 17.
Do Problems 4-(2 & 5) and 7-(1 & 4).
For Problem 4-5.a, I think the way the the problem is stated in
the book is misleading.
The word "necessarily" is meaningless, and they shouldn't
anthropomorphize the chips by talking about them
"conspiring".
I would rewrite it this way:
Give an argument why good and bad chips are indistinguishable.
I used graph theory ideas to do this in my solution, but
there are other ways.
For Problem 4-5.b, describe a strategy that takes
n chips with majority good, makes ⌊n/2⌋ comparisons,
and results in a subset of no more than n/2 chips
also of majority good.
Then give a proof that your strategy maintains a majority good.
Give a "complete" solution for Problem 4-5.c, that is,
code up a solution in a language of your choice, demonstrate correctness
with JUnit tests, give a correctness proof, and an analysis.
(The problem as stated in the text essentially asks for the correctness
proof.)
You can find my stub and some Junit tests
at
For 7-1, here is a lemma that makes several parts easier:
The significance of Problem 7-4 will be clearer to those who have taken
Programming Language Concepts.
If you haven't, you may want to discuss the problem with someone who has.
Problem 7-4.a is interesting (ie, complicated)
because it involves both recursion and a loop.
Due Sept 26
Daily Sep 19.
Do the following problem:
A stub plus two unit tests in python can be found
at
Daily Sept 19.
Do the following problem (based on a problem by Susanne Hambrusch, 1998):
A stub plus two unit tests in python can be found
at
HW Sep 24.
Do Problems 8-4, 15-(4 & 6).
Each of them are intended to be "complete":
implement a solution, write unit tests for it,
prove (something about) its correctness, and
analyze its efficiency.
But here are specific ways to adapt the idea of a "complete solution"
to these particular problems:
Due Oct 3
Daily Sept 26.
Read Sec 16.3. The premise is review, since the Huffman encoding
is covered in DMFP.
Our focus will be on the greedy choice property and
other aspects of correctness and efficiency.
Do Exercises 16.3-(2 & 4).
HW Oct 10.
Do Problem 16-2 and 17-2.
These are in the spirit of "complete" problems, but I'll
specify below what to prove etc.
Make sure you read the problems in the book before reading
my elaborations, since I'm going to assume you have a basic idea
of the premise of each problem.
For Problem 16-2
I have provided starter code, and one JUnit for each
part, found at The constraint for part a is merely that all tasks are executed,
which doesn't require any enforcement.
The constraint for part b is that all tasks are completed and
that no task is executed before it is released.
Do not assume that it is possible to schedule the tasks in
such a way that the processor is always busy. For example,
if the tasks have running times 3, 4, 9, and 1 but
release times 0, 5, 6, and 7, respectively, then after the 3-cycle task
is finished executing, the other tasks haven't even been released yet,
and so the schedule would need to include some idle time
until another task is ready.
(Obviously you want your schedule to include as little idle time as possible).
For the correctness proof in each part, explain what the
subproblem is and what the greedy choice is, and then
prove that the problem has the greedy choice.
Recall the structure of proof like that: suppose a solution
for a given subproblem
exists that doesn't use the greedy choice; construct a solution
based on that supposed one but that does use the greedy choice;
show that your constructed solution is as good as or better than
the supposed solution.
You should also demonstrate correctness with simple JUnit tests,
and you should analyze the running time of your solutions.
For Problem 17-2, I have provided starter code found
For part a, implement the helper method
For part b, implement the helper method
For part c, describe a strategy for deletion. You do not
need to implement
Finally, implement the iterator. I suggest the
iterator's state have variables
Due Fri, Oct 19.
B Tree exercise.
Instead of homework on B trees, we are turning this into
an in-class activity in which we will complete an implementation
of a B tree class, focusing on insertion.
Find the starter code at Specifically, If you have time after writing these, then write test cases
that exercise the code on large amounts of data.
Extra credit if you write legitimate test cases
that break my solution.
Turn your
HW Oct 19.
Do Problem 30-1.
Starter code in Python can be found at
Then implement the Graham's Scan algorithm (CLRS pg 1031)
in the code base found in
Due Wed, Oct 31.
HW Nov 12.
Do problems 3.1.10.(a & b) and 4.1.(8-10) in Lewis and Papadimitriou. For 3.1.10, notice that the preamble to
this problem gives a definition of regular grammar
in terms of a special case of a context free grammar.
We already know what a regular language is.
For part b, you need to prove that a language is regular
(old definition) if and only iff
there exists a regular grammar (new definition) for it.
Keep in mind what we already know---if a language is regular,
we know there is a RE and DFA and NFA for it, you can pick
which is most useful.
Also, Example 3.1.5 (pg 119) can be used as a hint---to an extent.
First, Example 3.1.5 constructs a grammar in which the rules have
exactly one terminal followed by exactly one nonterminal;
regular grammars described in this exercise can have any number
of terminals, followed by a single nonterminal.
Second, Example 3.1.5 is not worked out as fully as this exercise demands.
I will grade your submission mostly on the structure of
your proof, but do the best you can on the details also.
Due Mon, Nov 19.
HW Nov 14.
Do problems 5.4.2.(c-i) in Lewis and Papadimitriou.
These are difficult.
I want to incentivize your writing good, complete proofs,
yet make allowance for the fact that not all of you will get all of them,
and at the same time disincentivize wild guessing and hand-waving.
Here are some principles to guide you.
Due Wed, Dec 5.
HW Dec 5.
Do Problems 7.3.4 (f & h) in Lewis and Papadimitriou
and Exercise 34.5-2 in CLRS.
The book instructions for LP 7.3.4 say "prove that it is NP-complete by
showing that it is the generalization of an NP-complete problem.
Give the appropriate parameter restriction in each case."
That seems to suggest a brief answer, "it's just like this other known
NP complete problem, just change this or that parameter to..."
But that is not my intention with this assignment.
You should do a complete NP-completeness proof for each of these
(where "each"= parts f and h, which are assigned; trying the others
wouldn't be a bad studying strategy, though).
That means, prove that the problem is in class NP, then that the
problem is NP hard by showing a reduction.
Of course, you may use a generalization or specialization of the problem
for the reduction. That just makes the problem a bit easier.
You still must do them proofs completely.
Same thing for the other problem assigned, CLRS 34.5-2.
Clarification on LP 7.3.4.f: The phrase "two nodes 1 and n"
means two distinct nodes. The phrase "not repeating any node
twice" should be read as "not repeating any node" or "not visiting any
node twice."
(Taken literally, "not repeating any node twice" means "not visiting
any node three times." I do not think that's what the authors intended.)
CLRS 34.5-2 is actually the same problem as LP 7.3.4.e, just stated
a little more clearly and with a different hint.
Note that what CLRS calls "3-CNF-SAT" is what LP calls "3-SAT".
Due Wed, Dec 12.
Show that if it is not known that more than
n/2 chips are good---that is, it's possible that half
or more are bad---then the professor cannot determine
which chips are good using any strategy based on this
kind of pairwise test.
~tvandrun/Public/cs445/c4p5j.
In particular, I've made some classes to represent the chips, good and
bad, being careful to make the difference between the two opaque
to the code using the algorithm.
Chip.java contains the code for the chips.
The stub for the algorithm is in Diogenes.java.
At the end of the first iteration of the while loop,
i = p.
Proof.
By assignment, i is initially p-1.
On the first iteration of the second repeat-until
loop of the first iteration of the while loop,
i is the incremented to p.
Since A[i] = A[p] = x, the
guard on the second repeat-until loop fails.
With no other changes to i, i = p
at the end of that first iteration of the while loop.
You are playing a computer game in which the hero must pass through a series of
rooms and halls collecting treasure.
There are 2n rooms (in pairs) and
n-1 halls interspersed between the pairs.
Each room has a one-way door to the next hall,
and each hall has two one-way doors to the rooms of the next pair.
The hero must, therefore, pass through exactly one room in each pair.
The area looks something like
Each room has a certain amount of treasure, Ti,j.
Halls do not have treasure, but they each have a guardian
who demands payment
to let the hero cross diagonally through the hall.
So, to move from Ti-1,0 to Ti,0
is free, but to move from Ti-1,0
to Ti,1
costs
Pi.
T3,0 T3,1 P2 T2,0 T2,1 P1 T1,0 T1,1 P0 T0,0 T0,1
Devise and implement an algorithm to find the route that yields
the most treasure. Analyze its efficiency.
~tvandrun/Public/cs445/suppdynp/suppdyn/hero.py.
A lumberjack has an k-yard long log of wood he wants
cut at n specific places j1,
j2, ...
jn, represented as the distance of that
cut point from one end of the log.
(We can also consider the ends as trivial "cut points"
j0 = 0 and jn+1 = k.)
The sawmill charges $x to cut a log that is x yards long
(regardless of where that cut is).
The sawmill also allows the customer to specify the ordering
and location of the cuts.
For example, if k = 20 and we want cuts at 3 yards,
6 yards, and 10 yards from the left end, then if we cut them
from left to right the cost would be
20 + (20-3) + (20-6) = 20 + 17 + 14 = 51
But making the same cuts from right to left would cost
20 + 10 + 6 = 36
Devise and implement an algorithm to minimize the cost, and
analyze its running time.
~tvandrun/Public/cs445/suppdynp/suppdyn/sawmill.py.
For problem 8-4, I have provided a code base in Java
that you may complete:
~tvandrun/Public/cs445/c8p4j.
It has a class c8p4.Jug with nested classes Jug.Blue
and Jug.Red set up so that you can compare a red jug
with a blue jug, but not two jugs of the same color.
The class c8p4.TestJugSort is set up so that you can easily
add test cases that will apply to both parts (a) and (c).
For problem 8-4(a), you may finish the stub
JugSort.jugSelectionSort().
State an invariant for each loop, but you do not need to write proofs for them.
You may explain the Θ(n2)
comparisons by comparing your solution to a known sorting algorithm rather
than analyzing it from scratch.
For problem 8-4(b), use Theorem 8.1 or its proof.
For problem 8-4(c), don't worry about making the
algorithm "randomized," just shoot for the expected
case O(n lg n) number of comparisons.
You may finish the stub
JugSort.jugQuickSort().
State an invariant for each loop, but you do not need to write
proofs for them.
You may explain the number of comparisons by comparing your solution to a known sorting algorithm rather
than analyzing it from scratch.
For problem 15-4, I have provided a code base in Java
that you may complete: ~tvandrun/Public/cs445/c15p4j.
Specifically, your solution would complete the stub
c15p4.NeatPrint.neatPrint().
This method takes a string (presumably long and with no newlines)
and a line length.
It returns a string like the one given but with newlines inserted.
You can test this informally using the main method of NeatPrint.
For example,
java c15p4.NeatPrint gettysburg 50
will print the contents of the file gettysburg
to the terminal with lines of length 50.
Formal testing would be done with c15p4.TestNeatPrint,
which you can easily add test cases to.
However, you'll need to know ahead of time what the minimum
penalty is for the given text and line length.
So for writing your own testcases, I suggest working out
a few small examples by hand
(which is a good practice for unit testing anyway).
Instead of writing and proving invariants for your loops,
state the recursive characterization of your solution,
explaining what the variables mean as explicitly as possible.
In your code, document the tables you use, again explaining
what they mean as explicitly as possible and linking them to
your formal recursive characterizaton.
The analysis of its runtime shouldn't be difficult.
For problem 15-6, I have provided a code base in
Java that you may complete: ~tvandrun/Public/cs445/c15p6j.
It includes an implementation of the company structure
as described in the second paragraph of the problem:
The class c15p6.PersonnelTree is used to represent
a person, and a person has a link to one peer and one subordinate.
To make things easier, I have provided a way to iterate over a person's
subordinates, a way to retrieve the person's conviviality,
and a factory method which takes a string
representing the company tree/forest.
For example,
PersonnelTree.factory("(18(6(2)(3))(5(8)(1(10)(12))))")
produces the corporate structure
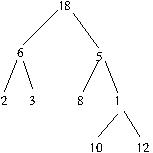
In that case the most convivial guest list is
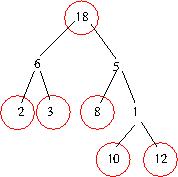
The class c15p6.PersonnelTree also has
a public instance variable aux which you
can use to annotate the nodes in the tree.
You may complete the stub c15p6.PartyPlanner.makeGuestList().
As with the previous problem, instead of loop invariant,
describe the recursive characterization
carefully and indicate the linkages between that
characterization and the tables in your code.
Write unit tests for small examples you can figure out by hand.
The analysis will probably not be difficult.
~tvandrun/Public/cs445/c16p2j.
Note that the output of a solution to part a is much simpler than
that of part b.
My stub for part a is void; the assumption is that the method will
merely rearrange the given array of tasks into an optimal order.
Part b somehow must construct a schedule indicating what portion
of which tasks to run in what order.
The suggestion implied by my stub is to return an ordered collection
(such as an ArrayList) of "schedule units", each
of which indicates a task to run and the length of time given
to that task before it is preempted.~tvandrun/Public/cs445/c17p2j.
The
class DynamicBinarySearchSet is set up to implement the
same Set interface as we used in CSCI 345. I have also provided the
whole suite of testcases for sets from that class, which you can use
through DBSSTest.
You do not need to write your own
testcases.
My apologies that those testcases are not separated into
testing the different parts of this problem. Also, you won't be able to
test part a much until part b is also done.
Notice also that n is stored in a byte, so
there can be at most 8 arrays.search(),
which
containsKey() and other methods use.
Write an invariant for each loop (in the code is fine, I've provided
some examples of [what I consider] good invariants in the given code).
Find the amortized time of your implementation, and show
how you determined it.
add(), for
which
I suggest you write the helper method merge(), whose
stub is provided.
Write an invariant for each loop you write.
Find the amortized time of your implementation, and show
how you determined it.
delete() (I haven't gotten around to
it myself), but if you want to just for fun, you can test it with
DBSSRTest.
Find the amortized time of your strategy, and show
how you determined it.
i and j where
i, j is the location of the next item to return,
unless the iteration is finished, in which case i is 8.
In other words, I hightly recommend you set things up so that
hasNext() is a one-liner and that in next()
advances the state of the iterator to prepare for the following call
to next()
~tvandrun/Public/cs445/btreej.
This exercise will feel very much like a CSCI 345 project.
BNode.split(), which
copies about half keys and values from a node to a new sibling.
Leaf.insertNonFull(),
which inserts a new key into a leaf node on which the method is
called, with the precondition that the node is not full
and thus could take this key/value without being split.
Internal.splitChild()
Internal.insertNonFull()
which inserts a new key
and value into a subtree rooted at the node on which the method is
called, with the precondition that the node is not full.
BTreeMap.iterator().
There is more than one way to do this, but the recommended way
(which the given code provides a context for) is to
maintain a "breadcrumb" stack indicating the trace
of nodes on the path to the current position.
BTreeMap.java file to
/cslab/class/cs445/(your user id)/btree.
This will count towards your participation grade (not towards homework).
~tvandrun/Public/cs445/c30p1p.
I have a fair amount of explanation for the parts of this problem and
a few hints, but I put them
in this separate document.
Please read the problem as it appears in the book first, then
read my hints and elaboration.
Also, if you want some help working through the fairly dense algebra,
please ask.
~tvandrun/Public/cs445/c33examplesj,
or implement it from scratch in a language of your choice.
In the given code base, your task is to implement
the initialization of the algorithm
in GrahamScanner.reset()
and one iteration of the main loop in
Graham.Scanner.actionPerformed()
A proof that a problem is decidable is simply an algorithm
that decides it.
You may describe the algorithm in any reasonable way:
As a Turing machine, in pseudo-code, etc.
Thomas VanDrunen
Last modified: Wed Dec 5 10:40:36 CST 2018